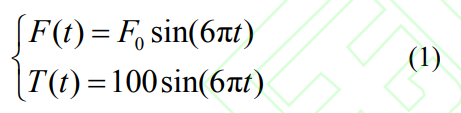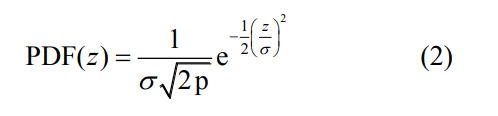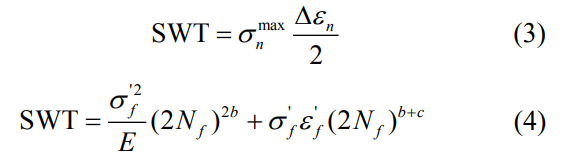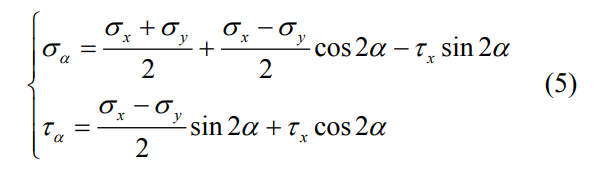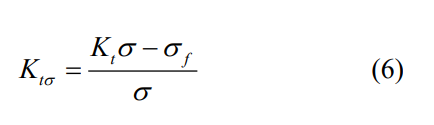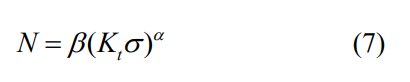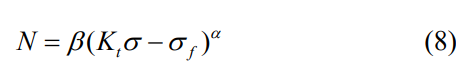当特种车辆行驶在复杂路况时,车轮承受的大量冲击载荷由承载轴传递至悬挂系统其他弹性元件并被吸收,车体所受冲击减小[1]。在此过程中承载轴承受较大的随机弯曲扭转复合载荷,易发生疲劳断裂。承载轴材料一般选用具有高强度的镍铬钢,为满足轻量化需求,具有较高比强度的钛合金也逐渐用于制造承载轴,如TC10、TC11、TC27等[2]。
改善钛合金承载轴疲劳寿命是提高车辆工作寿命、降低使用成本的有效手段。疲劳裂纹通常起源于材料表面或次表面,疲劳行为与材料表面完整性密切相关[3]。例如,残余压应力可以抵消部分外加载荷的不利影响,降低平均应力,提高裂纹萌生抗力,阻碍疲劳裂纹扩展;表面粗糙度较高的表面应力集中程度较高,导致疲劳寿命降低;微观结构与显微硬度等则会影响材料强度,从而影响疲劳寿命。
Wu[4]等研究了铣削-喷丸强化复合加工对TC11钛合金表面完整性及疲劳性能的影响,疲劳性能对刀痕更为敏感,精铣通过去除刀痕可以有效减少裂纹形核位点。Ren等[5]采用不同的滚压工艺对TC27钛合金进行强化,试样表面粗糙度、显微硬度、残余应力等指标均得到优化,试件疲劳寿命得到显著改善。
Gu等[6-7]研究了激光冲击强化对TC4钛合金共形接触微动疲劳寿命的影响以及表面结构对裂纹形核的影响,激光冲击强化增加了残余压应力的影响层深,在1.0×107次循环载荷下,寿命提高了70.4%,表面偏度和峰度较高的区域更利于裂纹形核。为了更高效地研究结构件多轴疲劳寿命的影响因素,学者们采用有限元仿真的手段建立了多种寿命预测模型。临界平面法是多轴疲劳理论与寿命预测的最显著进展,在多轴疲劳寿命预测研究中占据主要地位。Findley[8]最早提出了临界平面的概念,将剪切应力作为裂纹萌生和扩展的主要控制参量。Brown等[9]认为正应变加速了裂纹萌生,在预测疲劳寿命时正应变与剪应变应同时考虑。Socie等[10-11]提出了在最大剪切平面上以法向应力作为损伤参量,并在考虑了多轴附加硬化效应与平均应力的情况下提出了Fatemi-Socie(FS)寿命预测模型。对于拉伸型失效,Smith等[12]考虑了最大正应力与最大正应变的综合作用,提出了以最大正应变平面为临界平面的Smith-Waston-Topper(SWT)寿命预测模型,能够较为准确地预测拉伸型失效疲劳寿命。甘磊等[13]基于SWT模型提出两个新的能量参数,针对不同材料与不同疲劳形式建立了统一的多轴疲劳寿命预测模型,此模型预测精度较高。Song等[14]将表面形貌与残余应力引入二维有限元模型并利用SWT与FS模型预测TC4微动疲劳寿命,应力分量的相位差、主应力方向以及应力梯度是影响裂纹萌生的主要原因,较高表面偏度和峰度加速了裂纹的萌生。临界平面
法预测多轴疲劳寿命现已取得一定的研究成果,但目前研究大多是基于零件宏观结构受载与材料属性进行寿命预测,而机械加工造成的表面完整性的改变对疲劳寿命的影响研究较少,如何在寿命预测中引入表面完整性指标从而指导工艺优化,仍需进一步研究。
本文以某型承载轴材料TC11钛合金为研究对象,建立了弯扭载荷作用下的宏观受载有限元模型以及包含表面粗糙度与残余应力的微观有限元模型,采用SWT模型对TC11弯扭疲劳寿命进行预测,研究表面粗糙度与残余应力对弯扭疲劳寿命的影响规律;采用车削与超声滚压两种工艺加工的试样进行疲劳实验,验证模型预测的准确性,对比两种工艺下试样表面完整性并研究断裂机理。
1、研究方案
1.1 研究材料
材料为 TC11 (Ti-6.5Al-3.5Mo-1.5Zr-0.3Si) 钛合金,主要化学成分见表 1。主要组织为 α+β 双相结构,其中 α 相为主相,材料背散射电子形貌 (Backscatter Electron,BSE) 如图 1 所示,晶粒尺寸最大不超过 30μm。锻态室温力学性能见表 2。疲劳试样毛坯规格为 Φ21mm×250mm。
表 1 TC11 化学成分
Tab.1 Chemical composition of TC11
| 元素 | O | C | Al | Mo | Zr | Si | Fe | Ti |
| w /% | 13.5 | 9.1 | 6.1 | 1.0 | 0.5 | 0.2 | 0.1 | Bal |

表 2 锻态 TC11 钛合金室温力学性能
Tab.2 Mechanical properties of wrought TC11 titanium alloy at room temperature
| 抗拉强度 | 屈服强度 | 断面收缩率 | 断后伸长率 | 弹性模量 |
| /MPa | /MPa | /% | /% | /GPa |
| 1380 | 1098 | 23 | 8 | 123 |
1.2 包含表面粗糙度与残余应力的有限元建模
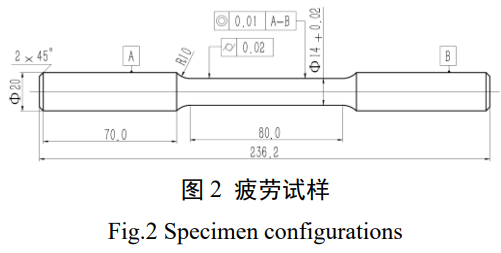
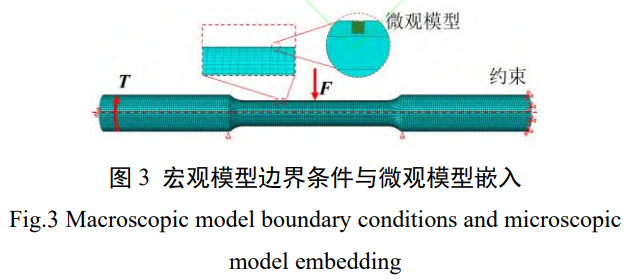
表面粗糙度的尺度一般为微米级,在宏观模型上难以模拟真实的微观表面形貌,因此需要建立微观模型并导入边界条件。首先完成宏观结构的有限元建模,宏观模型如图 2 所示,后续研究中的疲劳试样也采用此结构。
模型在 ABAQUS 中建立,如图 3 所示,一端完全固定约束,另一端约束除轴向外的另两个方向,两侧圆弧终点处限制竖直方向的自由度。在试样一端施加扭矩 T,中部沿法向施加集中力 F,具体如下:
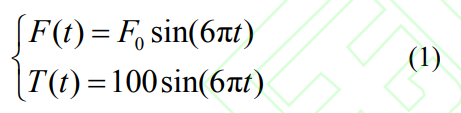
式中:F0 为不同水平的集中力初值,扭矩与集中力加载相位角插值为 0° ,即同相加载;微观模型为边长为 100μm 的立方体,网格尺寸设置为 2μm,共生成 125000 个 C3D8 六面体网格,将其嵌入宏观模型表面,并将同一坐标系下的宏观模型的位移映射到微观模型表面,作为其边界条件。
由于微观模型尺寸远小于宏观模型,因此并未考虑试样圆柱面引起的表面曲率,微观模型在应用宏观模型边界条件时产生的偏移可以忽略不计。面粗糙度 Sa 为表面的平均高度偏差,是一定区域内高度偏差的平均值,微观模型中的表面粗糙度在 ABAQUS 中由插件生成,以 S3 为指标设置 0.4、0.8、1.6、3.2μm 4 个水平。高度分布作为曲面生成算法,模型表面单元的高度信息服从高斯分布,即
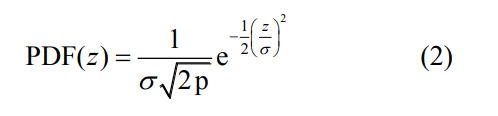
式中:σ 为标准差,z 为表面单元的高度。本文中实际零件的加工工艺为车削与超声滚压,建模时通过设置模型轴向与周向的采样点数进行样条插值,模拟刀痕结构 [15]。残余应力由预应力场施加,对微观模型在深度方向分层,逐层施加轴向与周向残余应力并通过一个空分析步平衡,模拟真实加工材料表层及次表层的残余应力勺型分布状态。表面粗糙度与残余应力设置见图 4、5。
1.3 SWT 寿命预测模型
采用 SWT 参数来评估材料在弯扭载荷下的疲劳,该参数定义为最大拉应力与最大应变幅的乘积。SWT 参数计算公式如下:
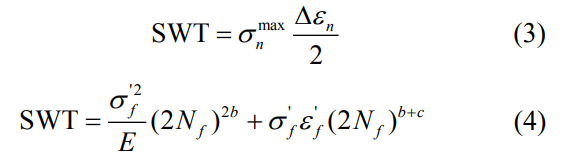
式中:E 为材料的弹性模量,σnmax 为临界平面上的最大法向应力,Δεn 为法向应变幅,Nf 为裂纹萌生寿命,σf、εf、b 和 c 分别为材料的轴向疲劳强度系数、轴向疲劳延性系数、疲劳强度指数和疲劳延性指数,材料参数见表 3。
使用临界平面法时,单元各个方向的 SWT 参数都需要用平面应力状态斜截面公式计算,将每个循环中每个单元的最大 SWT 作为最终输出。平面应力状态的斜截面公式可表示为
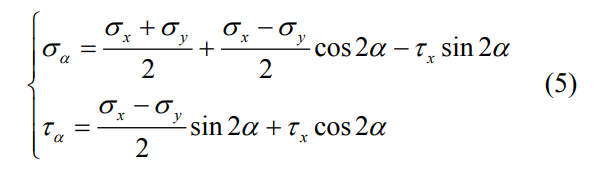
式中:σs、σy 分别为 x、y 方向的正应力分量,τx 为 XY 平面的剪应力,α 为斜截面法线与 X 轴的夹角。寿命预测模型中表面完整性具体因素水平设计见表 4,以表面粗糙度、表面轴向残余应力、表面周向残余应力为设计变量,每个因素分别设计 4 个不同水平,在每组有限元模型中除变动的参数外,其余表面完整性选取水平 2 的参数,即:Sa=0.8μm ,σa=-200MPa,σc=-200MPa。式 (1) 中 F0 取 21kN。
表 3 TC11 疲劳性能参数[16]
Tab.3 TC11 fatigue performance parameters
| E/MPa | σ'f /MPa | εf | b | c |
| 123000 | 1140.9 | 0.515 | -0.071 | -0.460 |
表 4 表面完整性参数设计
Tab.4 Surface integrity parameter design
| 组别 | 表面完整性指标 | 水平 | 水平数 |
| 1 | 面粗糙度 Sa/μm | 0.4、0.8、1.6、3.2 | 4 |
| 2 | 表面轴向残余应力 σa/MPa | -300、-400、-100、-200 | 4 |
| 3 | 表面周向残余应力 σc/MPa | -100、-200、-300、-400 | 4 |
1.4 弯扭疲劳寿命与断裂机理研究
将毛坯通过车削加工成如图 2 所示的疲劳试样,取部分车削试样超声清洗后进行超声滚压加工,采用两种试样进行弯扭疲劳实验。车削及超声滚压加工参数见表 5。
表 5 试样加工工艺参数
Tab.5 Sample processing parameters
| 切削速度 /(m・min-1) | 进给速度 /(mm・r-1) | 切削深度 /mm | 冷却润滑方式 |
| 50 | 0.10 | 0.20 | 微乳化切削液 |
| 超声振幅 /μm | 滚压速度 /(m・min-1) | 进给速度 /(mm・r-1) | 静载荷 / N |
| 3 | 0.10 | 200 | 5 |
使用基恩士 3D 激光共聚焦扫描显微镜 VK-X100 测量两种工艺下表面粗糙度并分析三维形貌。采用仪器压痕测试技术 [17] 表征材料局部显微硬度,在已加工试样上沿横截面切下待测样品,经镶块、研磨、抛光后,使用 MHVS-30AT 数显维氏硬度计进行硬度测试,选择金刚石正四角锥压头,负载大小为 4.9N,保荷时间为 15s。使用 Proto LXRD 微区应力仪,采用 X 射线衍射 (XRD) 的 sin2θ 法测量试样加工表面残余应力,选用 Cu-Kα 靶材,布拉格角 θ 选用 142°。使用非标实验系统进行弯扭疲劳实验,见图 6。

实验系统通过两个底座进行固定支撑,试样水平搭载在底座上,集中力加载头于试样中部施加垂直向下的交变载荷。试样两端通过联轴器与扭矩作用筒连接并承受扭矩。最大扭矩为 100N・m,最大集中力 F0 为设计变量,扭矩与集中力同相加载,应力比为 1/3,频率 3Hz。疲劳实验温度为 25℃,试样断裂后取下,统计疲劳寿命与预测寿命进行对比,验证预测模型的准确性。将断口切下后利用 SEM 电子扫描显微镜对疲劳断口的宏观及微观形貌进行观测,研究 TC11 在弯扭载荷下的断裂机理。
2、结果与讨论
2.1 疲劳寿命预测
图 7 为微观模型表面与截面的 SWT 损伤参量分布情况,材料表层 SWT 的分布情况取决于表面形貌,在车削刀痕的波谷处的值较大,在波峰处较小,疲劳裂纹萌生容易在波谷处产生,并在轴向拉应力作用下向材料内部扩展。在材料内部由于残余应力的勺型分布,不同层深处的 SWT 主要取决于残余压应力的大小,在图 5 的设计中,材料表层与 60~100μm 处的残余压应力水平较小,然而在材料表层由于表面粗糙度产生的应力集中效应,裂纹依然更容易在表层产生。
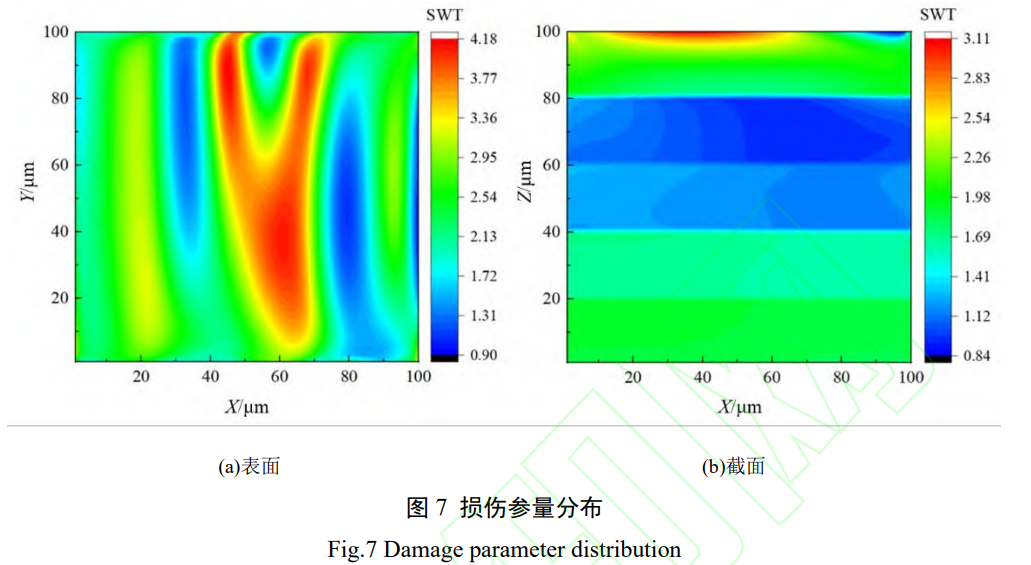
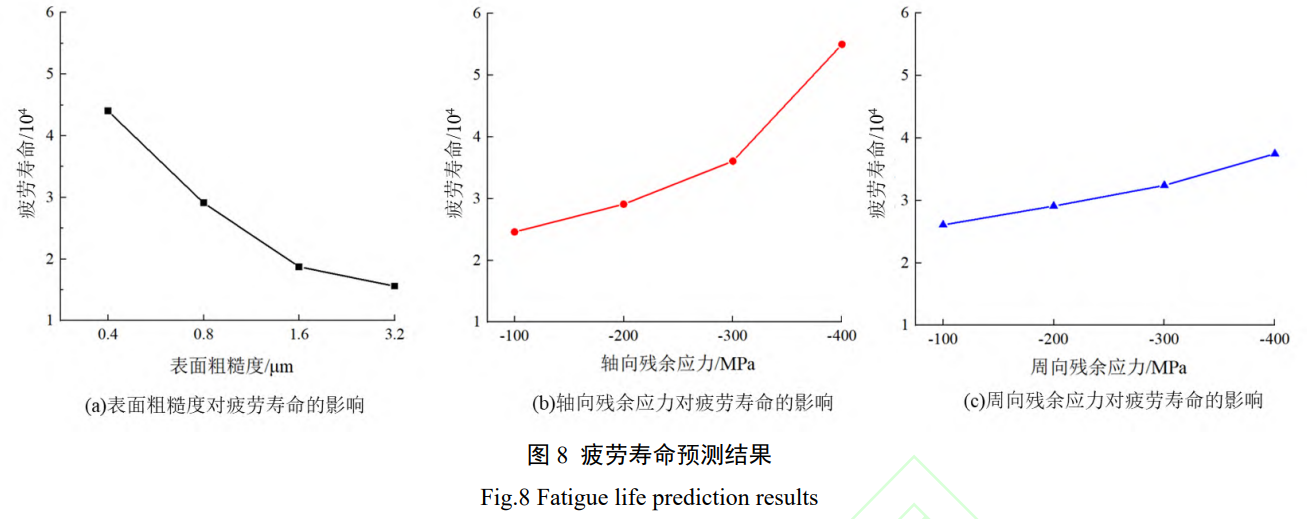
图 8 为不同表面完整性指标下的疲劳寿命预测结果。表面粗糙度 S3 由 3.2μm 降至 0.4μm,寿命提高了约 182%。在循环交变弯扭载荷作用下,加工表面轮廓的波谷位置产生应力集中,从而诱发表面的疲劳裂纹萌生。随着表面粗糙度增大,应力集中程度增大,裂纹尖端应力强度因子增大,达到应力强度阈值,疲劳裂纹更早萌生并开始扩展,使得疲劳寿命降低。随着轴向残余压应力由 100MPa 增大至 400MPa,寿命提高了约 123%。机械加工过程中在材料表层引入残余拉应力对疲劳寿命与疲劳抗力是有利的,在裂纹萌生阶段,残余压应力的引入能够与表面应力集中导致的局部应力相互抵消,延缓裂纹萌生速度,进而提高总疲劳寿命。何少杰 [18] 提出一个量纲一的变量
s=σf/σ
用于表示残余应力的影响,若不考虑材料塑性变形,外部载荷产生的应力与残余应力相叠加,此时考虑残余应力的应力集中系数应为
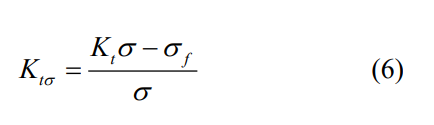
式中,Ktσ 为考虑残余应力的应力集中系数,K 为零应力状态下的应力集中系数,σ 为外部应力,σf 为表面残余应力。根据 Basquin 能量准则计算裂纹萌生寿命的公式为
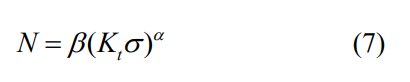
式中,β 为材料性能系数,将式 (5) 中修正后的应力集中系数代入 (7) 得到:
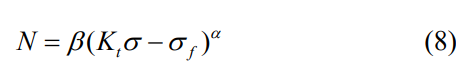
当材料表面存在残余压应力时,裂纹萌生寿命随残余压应力的增大而增大,轴向残余压应力与周向残余压应力的增大都能够提高零件的总疲劳寿命。周向残余应力由 100MPa 增至 400MPa,疲劳寿命提高了约 43%。实际加工中,表层材料精车后表面粗糙度一般为 0.8~1.6μm,滚压后表面粗糙度一般为 0.4~0.8μm。预测模型中随着表面粗糙度由 1.6μm 降低至 0.4μm,寿命提高了约 135%,与轴向残余压应力对寿命的影响程度相近。表面粗糙度与轴向残余应力对弯扭疲劳寿命影响显著程度高于周向残余应力。因此在工艺优化中,应以表面粗糙度与轴向残余应力为主要优化目标,周向残余应力为次要优化目标。
2.2 疲劳试样表面完整性与寿命
不同工艺加工的疲劳试样表面粗糙值见图 9。
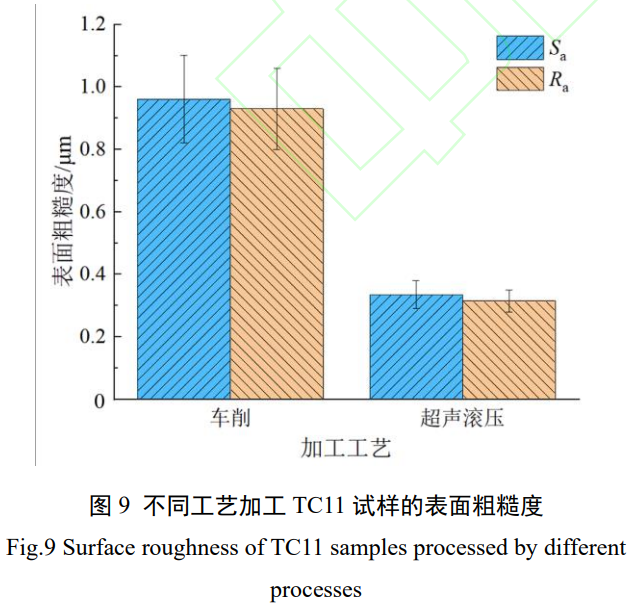
图 9 中与车削工艺相比,滚压试样表面粗糙度降低了约 64%。对不同工艺下试样表面的三维形貌进行表征,见图 10。
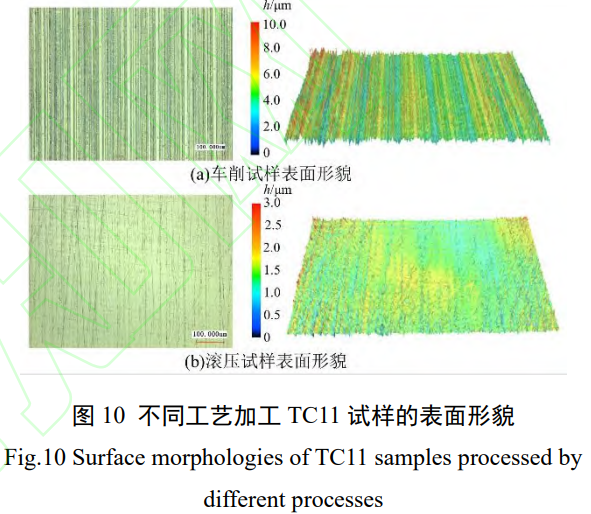
图 10 中车削试样有明显的由车削产生的凸峰和凹谷,且分布较均匀,最高位置与最低位置的高度差约为 8μm。经超声滚压加工后,试样表面的车削痕迹明显减弱,表面粗糙度显著降低,表面相对平整,最高位置与最低位置相差仅为 3μm。 不同工艺加工的试样显微硬度 (见图 11),车削试样表层显微硬度约为 380HV0.5,加工硬化程度 NH 约为 111.8%。显微硬度沿深度方向先增大后减小,在距表面约 150~200μm 的位置,显微硬度达到最大值,约为 400HV0.5。随深度增加显微硬度逐渐减小最终趋于基体硬度,硬化层深度约为 0.7mm。滚压试样表层硬度较车削有显著提高,约为 400HV0.5。加工硬化程度 NH 约为 117.7%。
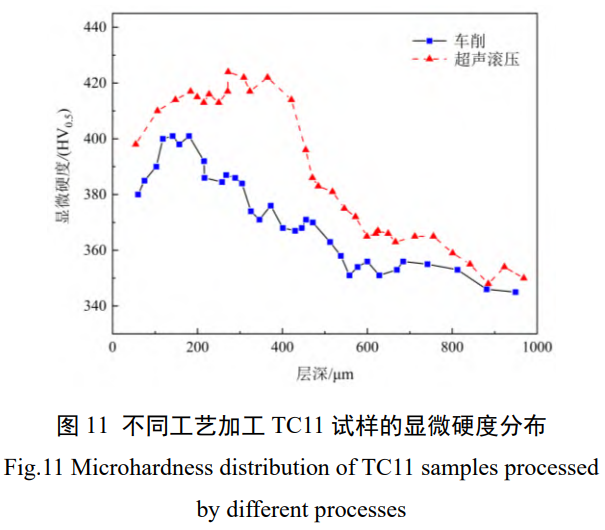
显微硬度沿层深的分布情况与车削试样相似,在据表面约 300μm 处硬度达到最大,约为 424HV0.5。硬化层深约为 0.9mm,较车削试样提高了 28.5%。 不同工艺加工的试样表面残余应力 (见图 12),超声滚压引入了更高的残余压应力,轴向与周向分别增大约 46.5% 和 31.8%。切削表层残余应力的形成是塑性变形与切削热的共同作用,切削完成后表层金属降温回弹,受次表层金属阻碍产生残余拉应力,同时表层金属塑性拉伸变形受次表层未发生塑性变形层的阻碍而产生残余压应力。
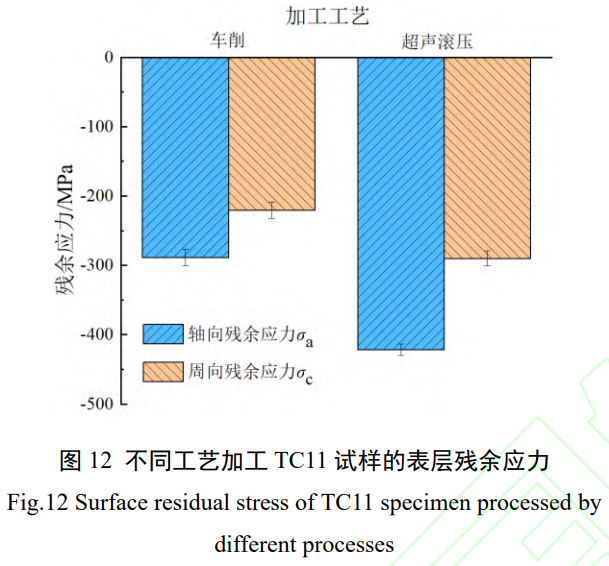
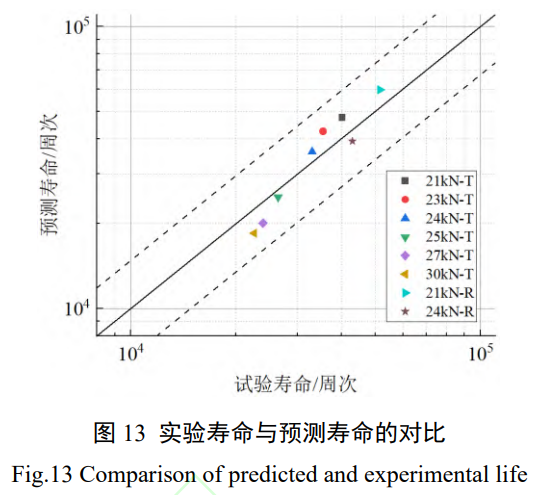
在滚压加工中,滚压头对材料表面施加压力造成严重的塑性变形,使晶粒滑动、拉长、破碎的过程中位错缠绕,从而在表层引入较大的残余压应力 [19-20]。 为验证预测模型的准确性,使用车削 (T) 试样与滚压 (R) 试样在 F0 为 21~30kN 条件下进行疲劳实验,统计断裂寿命并与预测寿命进行对比,结果见图 13,该模型在 25% 的误差范围带内能够较准确地预测弯扭疲劳寿命。
2.3 疲劳断口形貌
图 14 为车削加工 TC11 试样疲劳断口形貌,TC11 的弯扭疲劳断口分为疲劳裂纹萌生区 (①区)、裂纹扩展区 (②区) 和瞬时断裂区 (③区) 3 个区域。疲劳断面形状均较为平坦,裂纹萌生后以疲劳源为中心呈放射状向材料内部扩展,是典型的由单一裂纹源产生的疲劳破坏。裂纹源的表层可观测到明显的突起,疲劳裂纹形核初期张开的位移较小,随着裂纹向内部扩展与载荷继续施加进行反复开合,使得断口的两个界面不断进行挤压和摩擦,形成面积很小且比较光滑的摩擦区域。在裂纹扩展区存在撕裂棱和一些短小的撕裂痕迹,同时存在与裂纹扩展方向垂直的条带状结构,也称为疲劳辉纹,车削试样裂纹扩展区疲劳辉纹间距约为 0.8~0.9μm。
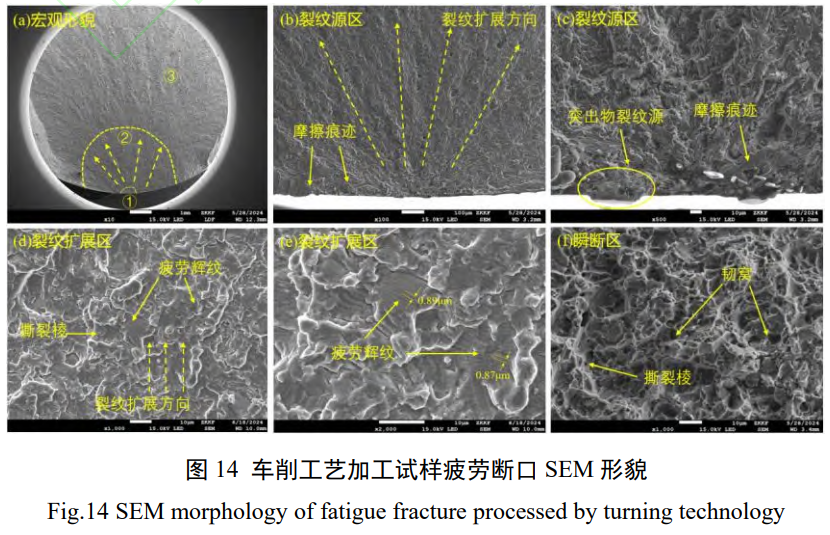
疲劳辉纹是交变应力循环裂纹尖端塑性钝化形成的微观特征,辉纹间距反映了裂纹扩展速率,间距越大扩展速率越快。瞬断区形貌比较粗糙,有大量的撕裂型韧窝存在,以及少量的撕裂棱,瞬断区的断裂方式为脆韧混合断裂,穿晶断裂和沿晶断裂两种形式同时存在,主要形式是沿晶断裂。
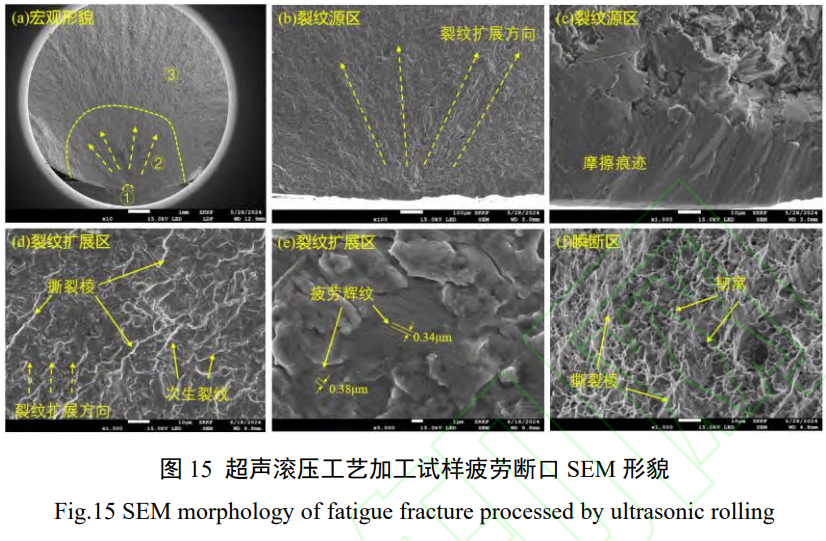
图 15 为超声滚压加工 TC11 试样疲劳断口形貌,由于滚压试样的疲劳寿命较高,受载循环周次更长,断面之间的挤压与摩擦更为严重,在裂纹源区形成了面积更大的较光滑的摩擦区域。在裂纹扩展区,与车削试样相比,疲劳辉纹间距大大减小,约为 0.3~0.4μm,同时存在着较多的撕裂棱与次生裂纹,呈现出更多的穿晶断裂特征。滚压试样表层具有更高的残余压应力,在受载时能够抵消更多外载荷的作用,导致裂纹扩展速率减缓,在断口形貌方面表现为更小的疲劳辉纹间距。在瞬断区分布着更多的撕裂棱,韧窝数量与尺寸减小,滚压强化对材料的形变强化使得材料在受载过程中塑性变形能力提高,TC11 的疲劳断裂形式仍为脆韧混合断裂。
3、结论
本文建立了 TC11 钛合金弯扭疲劳寿命预测模型,研究了表面粗糙度、表面轴向残余应力与表面周向残余应力对弯扭疲劳寿命的影响规律。验证了预测模型的准确性,并分析了不同工艺下试样的表面完整性以及疲劳断口形貌。得到结论如下:
表面粗糙度与轴向残余应力对弯扭疲劳寿命影响显著,随着表面粗糙度 S2 由 1.6μm 下降至 0.4μm,寿命提高了 135%;轴向残余压应力由 100MPa 增至 400MPa,寿命提高了 123%;周向残余应力由 100MPa 增至 400MPa,疲劳寿命提高了约 43%,周向残余应力对寿命的影响较小。
与车削相比,超声滚压试样表面粗糙度由 0.93μm 降低至 0.31μm,表层显微硬度由 380HV0.5 提高至 400HV0.5,硬化层深度提高了 28.5%,表层轴向与周向残余压应力分别提高了 46.5% 和 31.8%。SWT 模型能够在 25% 的误差范围带内较准确地预测 TC11 弯扭寿命。
在 TC11 的弯扭疲劳过程中,与车削试样相比,滚压试样疲劳裂纹萌生时间延长,裂纹扩展区疲劳辉纹间距由 0.8~0.9μm 降低至 0.3~0.4μm,扩展速率降低,在加工影响层呈现出更多的穿晶断裂特征。
参考文献
[1] XU Hongying, LI Jiaxing, LIU Jun, et al. Fatigue life analysis of balance elbow structure during firing [J]. Journal of Physics: Conference Series, 2023, 2460 (1): 012028. DOI: 10.1088/1742-6596/2460/1/012028
[2] 史文,李巍. ZTC10 钛合金平衡肘断裂分析 [J]. 失效分析与预防,2016, 11 (5): 300 SHI Wen, LI Wei. Fracture failure analysis of ZTC10 titanium alloy balance elbow [J]. Failure Analysis and Prevention, 2016, 11 (5): 300. DOI: 10.3969/j.issn.1673-6214.2016.05.007
[3] 高玉魁。表面完整性理论与应用 [M]. 北京:化学工业出版社,2014 GAO Yukui. Theory and application of surface integrity [M]. Beijing: Chemical Industry Press, 2014
[4] WU Zegang, ZHANG Dinghua, LI Jing, et al. Influence of milling-finishing-shot peening hybrid machining on the surface integrity and fatigue performance of TC11 titanium integral impeller [J]. The International Journal of Advanced Manufacturing Technology, 2024, 134 (9): 4539. DOI: 10.1007/s00170-024-14416-8
[5] REN Zhaojun, LAI Fuqiang, QU Shengguan, et al, Effect of ultrasonic surface rolling on surface layer properties and fretting wear properties of titanium alloy Ti5Al4Mo6V2Nb1Fe [J]. Surface and Coatings Technology, 2020, 389: 125612. DOI: 10.1016/j.surfcoat.2020.125612
[6] GU Huiqing, YAN Pei, JIAO Li, et al. Effect of laser shock peening on boring hole surface integrity and conformal contact fretting fatigue life of Ti-6Al-4 V alloy [J]. International Journal of Fatigue, 2023, 166: 107241. DOI: 10.1016/j.ijfatigue.2022.107241
[7] GU Huiqing, JIAO Li, YAN Pei, et al. Effect of machined surface texture on fretting crack nucleation under radial loading in conformal contact [J]. Tribology International, 2021, 153: 106575. DOI: 10.1016/j.triboint.2020.106575
[8] FINDLEY W N. A theory for the effect of mean stress on fatigue of metals under combined torsion and axial load or bending [J]. Journal of Engineering for Industry, 1959, 81 (4): 301. DOI: 10.1115/1.4008327
[9] BROWN M W, MILLER K J. A theory for fatigue failure under multiaxial stress-strain conditions [J]. Proceedings of the Institution of Mechanical Engineers, 1973, 187 (1): 745. DOI: 10.1243/pime_proc_1973_187_069_02
[10] SOCIE D. Multiaxial fatigue damage models [J]. Journal of Engineering Materials and Technology, 1987, 109 (4): 293. DOI: 10.1115/1.3225980
[11] FATEMI A, SOCIE D F. A critical plane approach to multiaxial fatigue damage including out-of-phase loading [J]. Fatigue & Fracture of Engineering Materials & Structures, 1988, 11 (3): 149. DOI: 10.1111/j.1460-2695.1988.tb01169.x
[12] SMITH K N, TOPPER T H, WATSON P. A stress-strain function for the fatigue of metals [J]. Journal of Materials, 1970, 5 (4): 767
[13] 甘磊,吴昊,仲政。基于能量法的多轴疲劳寿命预测方法 [J]. 固体力学学报,2019, 40 (3): 260 GAN Lei, WU Hao, ZHONG Zheng. Fatigue life prediction under multiaxial loading using energy-based models [J]. Chinese Journal of Solid Mechanics, 2019, 40 (3): 260. DOI:10.19636/j.cnki.cjsm42-1250/o3.2019.007
[14] SONG Yifan, YAN Pei, JIAO Li, et al. Numerical simulation of the effect of surface microgeometry and residual stress on conformal contact fretting fatigue crack initiation behavior [J]. Fatigue & Fracture of Engineering Materials & Structures, 2023, 46 (8): 2798. DOI: 10.1111/ffe.14033
[15] WANG Yuechang, AZAM A, WILSON M C T, et al. A comparative study for selecting and using simulation methods of gaussian random surfaces [J]. Tribology International, 2022, 166:107347. DOI: 10.1016/j.triboint.2021.107347
[16] WU Zhirong, HU Xuteng, SONG Yingdong. Multiaxial fatigue life prediction for titanium alloy TC4 under proportional and nonproportional loading [J]. International Journal of Fatigue, 2014, 59: 170. DOI: 10.1016/j.ijfatigue. 2013.08.028
[17] MOHARRAMI R, SANAYEI M. Developing a method in measuring residual stress on steel alloys by instrumented indentation technique [J]. Measurement, 2020, 158: 107718. DOI: 10.1016/j.measurement.2020.107718
[18] 何少杰。铣削加工表面疲劳应力集中系数分析与实验研究 [D]. 武汉:华中科技大学,2016 HE Shaojie. Analysis and experimental investigation of fatigue stress concentration factor of milled surface [M]. Wuhan: Huazhong University of Science and Technology, 2016
[19] ZHANG Z F, WANG Z G. Grain boundary effects on cyclic deformation and fatigue damage [J]. Progress in Materials Science, 2008, 53 (7): 1025. DOI: 10.1016/j.pmatsci.2008.06.001
[20] ZHAO Yangyang, GONG Baoming, LIU Yong, et al. Fatigue behaviors of ultrasonic surface rolling processed AISI 1045: The role of residual stress and gradient microstructure [J]. International Journal of Fatigue, 2024, 178: 107993. DOI: 10.1016/j.ijfatigue.2023.107993
相关链接