- 2025-04-30 22:05:33 热处理工艺对航空结构件用Ti-6Al-4V钛合金(TC4)组织与性能影响
电致塑性效应是指材料在通电条件下塑性变形能力提升的现象,其机理研究自MachlinES[1]的早期研究以来逐步深入。目前,研究人员已广泛认可焦耳热效应产生的温度场可降低变形抗力和提高延展性[2-4]。然而电致塑性研究的核心问题在于:除焦耳热之外的电致塑性效应有哪些?他们在变形过程中起到的提升塑性的作用贡献如何?部分研究认为,焦耳热效应足以解释脉冲电流对塑性的提高作用,除此以外,不存在非热的电致塑性效应。然而,其他研究人员则支持着非热电致塑性的存在,AndreD等[6]认为,相比于焦耳热效应,电致位错脱钉才是电致塑性效应最主要的机制。在众多的非热电致塑性理论中,电子风理论获得较为广泛的认可,该理论虽然早期预测得到的应力降低值过低[7],但经过ConradH[8-9]在总结相关研究经验的基础上提出,脉冲电流在高温下对塑性的提升主要归功于流动应力热分量的减少,且脉冲电流促进了热激活方程指前因子的增加,这一机制被认为是电致塑性效应中最显著的影响因素。
除此之外,局部焦耳热效应是否存在、该效应在流动应力降低和延伸率的提高占据多大比例?这些问题仍然需要进一步探索。在电致塑性变形试验研究中,往往会设置与电辅助变形温度相同的无电流纯热变形试验作为对照,通过比较两者的力学行为和微观结构变化判断电流的非热效应[10-13]。但是这种方法默认了脉冲电流产生的热场效果与无电流的纯热场相同,然而实际上,电子与位错等缺陷处的原子碰撞所传递的原子动能可能不同于电子与接近完美晶格位置的原子碰撞所传递的原子动能。名古屋大学的HosoiA等[14]认为由于裂纹处电阻高,会在局部产生更高的焦耳热。BhowmikA等[15]认为瞬态的局部焦耳热冲击和电子风力共同促进了位错的湮灭,并导致位错从晶界处脱离。但KimMJ等[16]持相反的意见,他们在模拟仿真中将晶界的电导率设定为晶内的0.001~0.1倍发现,由于热传导迅速,晶界处温度未产生明显的变化。正如前所述,电子与缺陷的作用产生了瞬时“热点”和局部焦耳热效应,其本征特性导致在宏观试验中往往只能改变大范围的平均温度场,无法影响局部缺陷的温度分布。因此,局部焦耳热效应难以从宏观焦耳热效应中分离出来并量化。通过分子动力学(Molecular Dynamics,MD)方法可以直接向不同位置的原子施加不同的原子动能,从而直接模拟脉冲电流带来的瞬时不平衡冲击。
为准确理解电致塑性机理,进而实现对各类电辅助加工工艺的控形控性,有必要探明局部焦耳热效应在电辅助变形中所占的比例。本文选取航空航天领域常用的Ti-6Al-4V钛合金作为研究对象[17],研究其局部焦耳热效应和电辅助U形弯曲的力学行为,借助分子动力学(Molecular Dynamics,MD)方法和宏观有限元法(Finite Element Method,FEM),使用多尺度的仿真得到各类电致塑性效应所占比例,并合成以预测电辅助加工工艺的成形结果。
1、研究方法
在微观尺度,通过构建含缺陷的Ti-6Al-4V模型,采用MD仿真方法研究电致塑性效应。通过设置等效能场,对比纯热场与局部动能增强条件下原子团纳观尺度的变化与其力学行为,以此分离并量化局部焦耳热效应的贡献。其中,缺陷处原子的动能被设置为其余原子的6倍,但保证总原子动能相等,以模拟电流在微观缺陷处引发的局部原子动能提升现象。
在宏观尺度,采用FEM方法仿真电辅助U形弯曲工艺。基于前期试验建立了考虑平均焦耳热与非热效应的应力-应变模型,对比实际电辅助弯曲试验结果,验证了该模型的预测能力。为实现更精准的预测,将MD仿真得到的局部焦耳热效应比例引入宏观应力-应变模型,形成跨尺度修正方案。具体研究流程如图1所示。
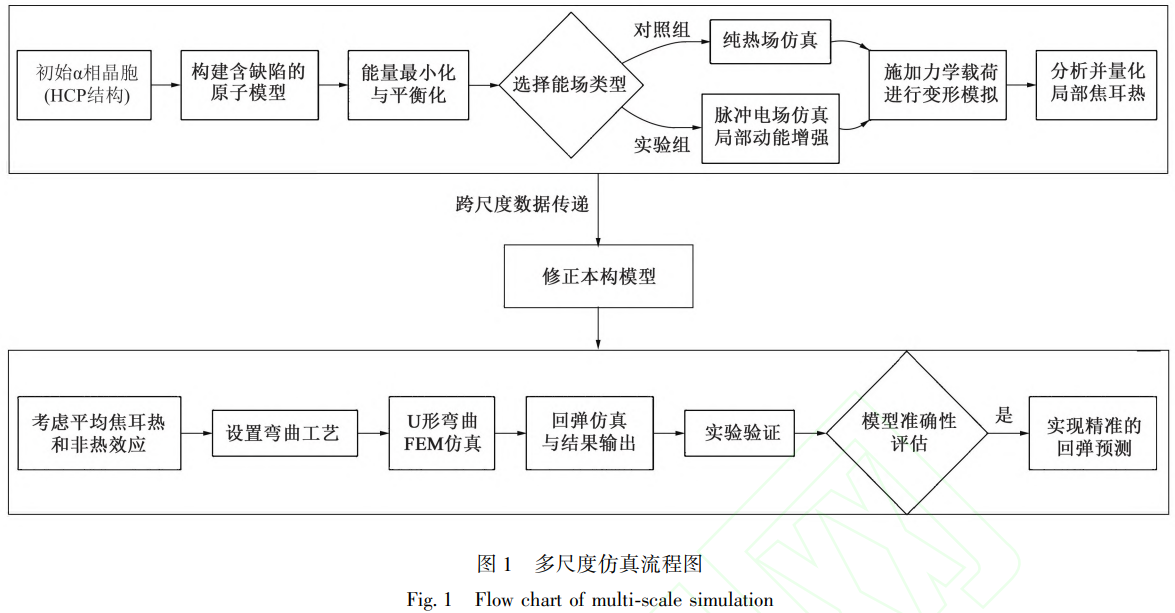
1.1分子动力学仿真研究方法
仿真过程中,初始原子均为Ti原子,然后将其中6%和4%(按质量分数)的Ti原子随机替换为Al和V原子。鉴于实际材料中α相约占比90%,仿真选用a相作为初始晶格结构。所有仿真均在上海交通大学π2.0超算平台上使用LAMMPS软件进行,时间步长设为1fs,采用周期性边界条件,每次仿真包含91200个原子。
原子模型通过Atomsk软件构建:以HCP单胞为基础,经正交化后单胞尺寸为2.91x5.04x 4.67A。为避免内应力过大,将单胞微调至3.0A 5.0x4.8 A;单胞内含有4个原子,并沿X、Y、Z方向分别扩展为40x24x25的晶胞阵列,共96000个原子;随后随机删除4800个原子以引入5%空位缺陷;最终模型含有91200个原子。在此基础上分别引入刃型位错和螺型位错,其中,刃型位错线沿Z轴方向排列,螺位错线沿X轴方向排列,二者柏氏矢量同为2.12A。
仿真初始将所有原子温度设为20℃的高斯分布,并进行能量最小化,然后在等温等压系统(I-isothermal-Isobaric Ensemble, NPT)下以不超过10 −3 ∘C ⋅ fs −1的速率将原子团升温至目标温度(20、171.1和600℃)。为研究脉冲电场的局部焦耳热效应,设置了纯热场和等效脉冲电场两种条件:(1)纯热场中原子温度按平均温度呈高斯分布;(2)脉冲电场通过势能识别高势能原子,将势能最高的1%原子定义为高势能原子,使其平均温度为其余原子的6倍,同时保持系统总动能与等效纯热场一致,以仿真电场导致的局部动能不均匀分布。
电场和热场的仿真过程在正则系综(Canonical Ensemble,NVT)下进行,沿X和Z方向施加真应变速率为10°s-1的拉/压应力。对于脉冲电场条件,每皮秒(ps-1)施加一次温度脉冲以更新原子动能分布。原子间相互作用采用基于Al-V[18]、Al-Ti[19]和V-Ti[20]的混合修正嵌入原子法(Modified Embed-ded Atom Method,MEAM)势函数进行描述,仿真结果采用Ovito软件进行可视化分析。
1.2FEM仿真研究方法及其跨尺度的修正
电辅助U形弯曲FEM仿真的模具形状如图2所示,该FEM仿真的物理过程如下:首先,将380mmx20mmx0.9mm的Ti-6Al-4V钛合金板料置于图2下方的凹模上,通入脉冲电流并将上凸模以10mm·min-1的速率下压,由于凸模和凹模对应位置的半径不同,凸模下行至其下底面与凹模上底面位置为 1.4 mm即停止,则实际下压距离为 50-1.4 = 48.6 mm。完成弯曲后,停止脉冲电流并向上移动凸模。对于此物理过程,在 FEM仿真中直接将上述模型预测的不同有效电流密度和温度对应的Ti-6Al-4V钛合金单轴拉伸曲线作为输入参数以获得板料在弯曲过程中的力学行为。FEM仿真中模具和板料均采用壳模型以在减少计算量的前提下保证精度。弯曲过程采用显式的拉格朗日算法,结果输出到 dynain文件中,再对弯曲后的工件进行隐式算法求解回弹。对比实际电辅助弯曲试验后工件的角度
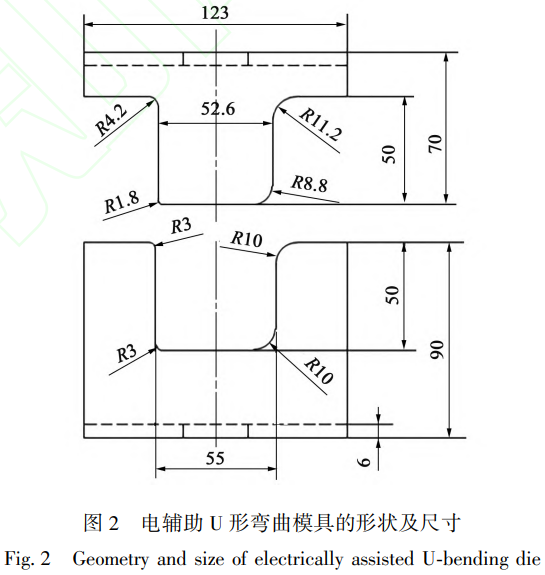
可评估仿真模型的准确性。由于仿真过程中板料的总热容远低于模具,因此设定其温度为与模具相同的室温。与常见的对称U形弯曲不同,在FEM仿真中所使用的模具为左右不对称,因此在圆角半径较小一侧应力和应变均更高,并且也不能使用常用的截取对称面一侧的方式进行仿真。
1.3 Ti-6Al-4V单轴拉伸应力-应变模型
文献[21]给出了Ti 2 AlNb钛合金的应力-应变理论模型,可预测电辅助单轴拉伸导致的应力降低。考虑到本文所述的 Ti-6Al-4V钛合金与Ti 2 AlNb钛合金原模型存在差异,对该模型进行了如下修正,使有效应力σ eff 从原模型的等于a 0 被修正为:

式中:a 1 和a 0 均为材料参数; T为平均温度。
根据式(1)的修正方法,相应地,总的脉冲电流导致的应力降低Δσ pulse 可从原模型中修正后,使用系数λ 2 、真应变ε、材料参数a 1 、b 1 以及有效电流密度 J描述为式(2):
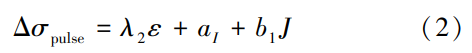
此时,系数λ 2 内含了温度影响的应变硬化的参数,而非原文的有明确物理意义的加工硬化率λ [21]。为了能够进一步使用已有的电辅助单轴拉伸的温度拟合参数,将内含温度影响的参数λ 2 表达为式(3):

式中:a 5 和a 6 为仅与材料相关的常数。
与试验数据拟合后,得到各参数的取值范围如下:a 5 = (29.1 ± 0.8)MPa ⋅ ∘C −1、a 6 = (8877.0±252.6) MPa、b 1 = (13.8 ± 0.8) (MPa ⋅ mm 2) ⋅A −1、a 1 = (−259.3 ± 8.3)MPa。拟合的决定系数R 2值为 0.96,可判断该理论模型对 Ti-6Al-4V钛合金电辅助单轴拉伸试验结果拟合良好。
2、研究结果
2.1 MD仿真结果
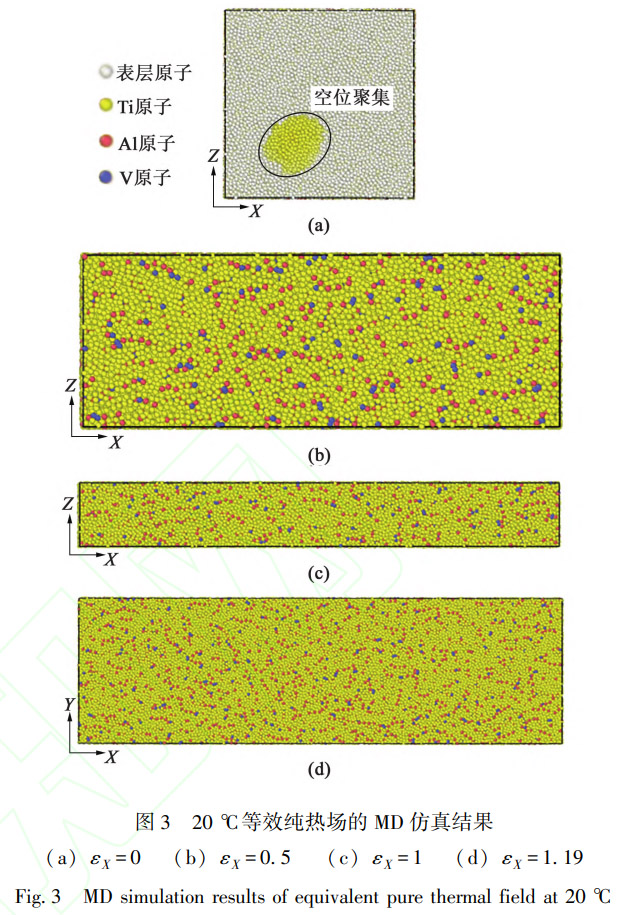
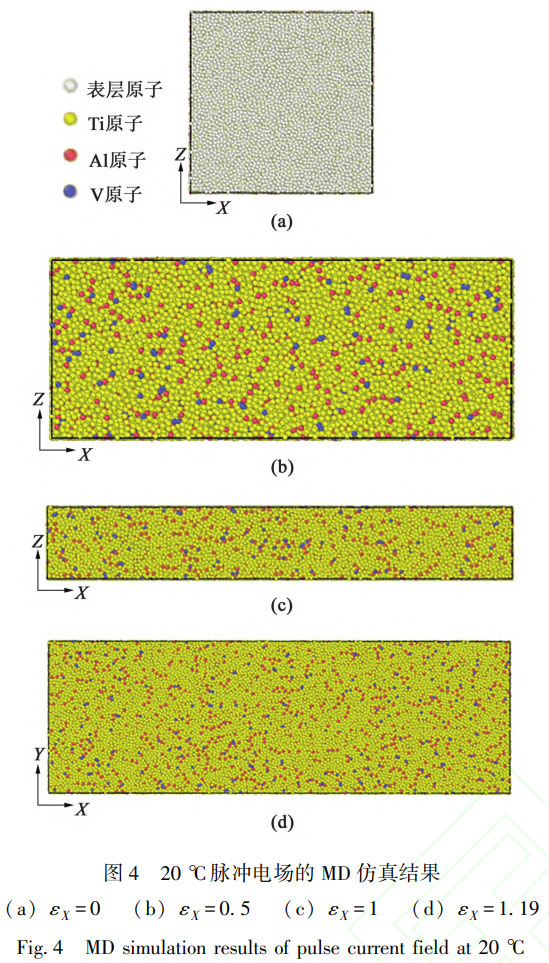
20 ∘C(室温)下沿 X轴方向拉伸、 Z轴方向压缩时,等效纯热场和脉冲电场的 MD仿真结果分别如图 3和图 4所示。原子团内引人的空位在纯热场作用下初始状态( X方向真应变ε X = 0)是集聚的(图 3a);而在脉冲电场作用下,可能由于高势能原子被脉冲电流赋予的高动能促进了原子之间的碰撞和运动,因此,在初始状态的极短时间内,电场作用下原子团就不再存在空位的聚集(图 4a)。当 X方向的真应变达到 0.5时,热场内的空位逐渐分散消失(图 3b),这说明室温下 X方向拉伸、 Z方向压缩的变形足以消除空位。当 X方向真应变继续增大至 1时,热场和电场内均未发现聚集的空位,也未发现位错(图 3c和图 4b∼图 4c),这意味引人的位错已经在变形过程中消失,且难以归功于局部焦耳热。当 X方向真应变达到 1.19时,也未再发生空位聚集(图 3d和图 4d),因此也不会导致断裂失效发生。
171.1℃下沿X轴方向拉伸、Z轴方向压缩时,等效纯热场和脉冲电场的MD仿真结果分别如图5和图6所示。两种外加能场的初始状态(ex=0)均没有空位聚集(图5a和图6a),这可能是由于温度
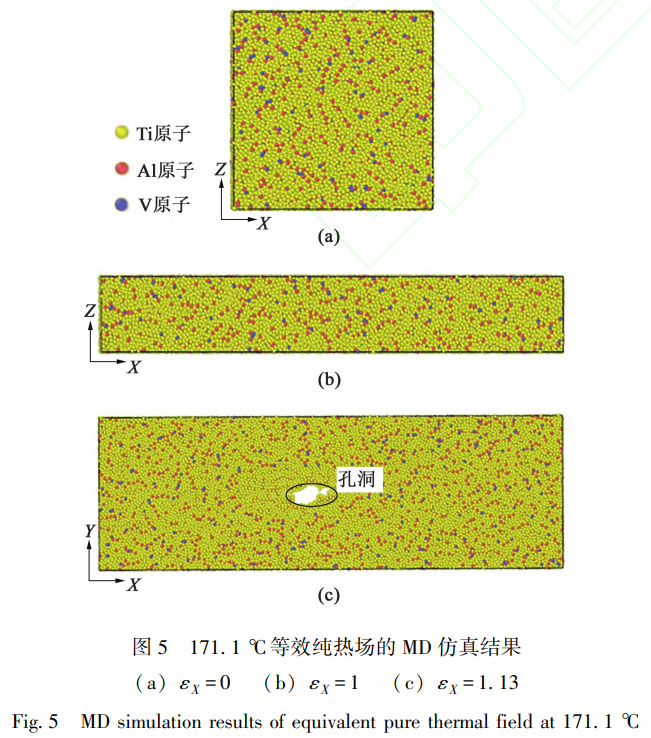
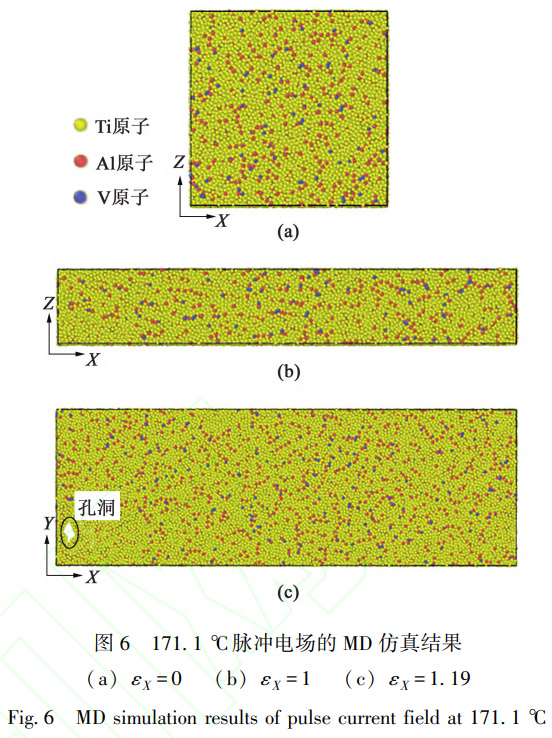
升高获得的能量有利于空位扩散,该现象符合金属温度升高,塑性增强的一般规律。与室温相似, X轴方向拉伸、 Z轴方向压缩,当 X方向真应变达到1时, Ti-6Al-4V钛合金仍未发生断裂失效(图 5 b和图 6b)。然而,随着真应变继续增加,纯热场下Ti-6Al-4V钛合金在 X方向真应变达到 1.13时,由于空位聚集而导致材料被孔洞穿透(图 5c)。在脉冲电场下相似的失效方式发生在 X方向真应变为1.19时(图 6c),说明同等温度下脉冲电场可得到更大的塑性变形量。
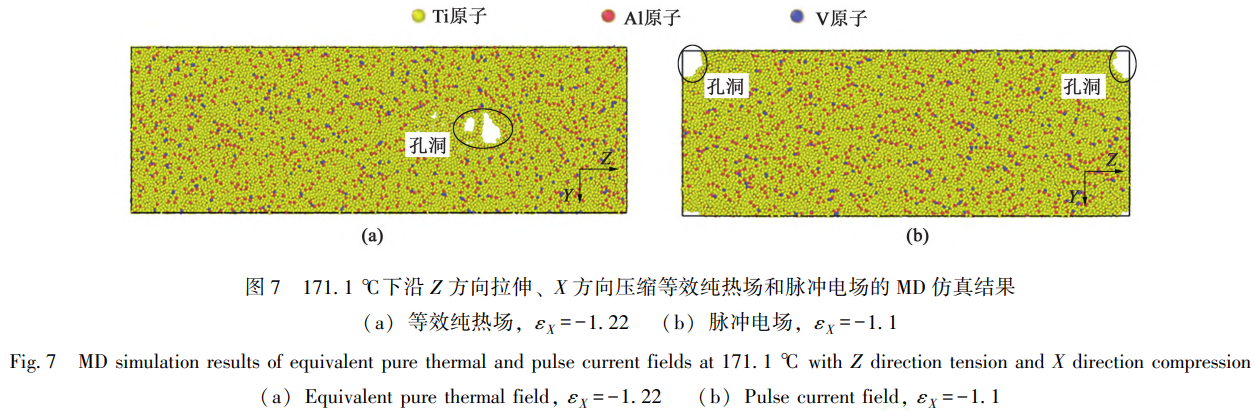
171.1 ∘C下沿 X方向压缩、 Z方向拉伸时,等效纯热场和脉冲电场的 MD仿真结果如图 7所示。纯热场相比脉冲电场为变形带来了更高的延展性,前者在 X方向的真应变达到-1.22时才发生空位聚集和穿孔断裂(图7a),但后者在相同方向的真应变为-1.1时失效就已经发生(图 7 b)。当变形温度为171.1 ∘C时,纯热场和脉冲电场的塑性差异表明局部焦耳热未必能够增强延展性。外加的不均匀热场对塑性影响可能与初始变形状态的晶格取向有关(即不同方向的拉伸或压缩变形),当宏观上材料为多晶,无明显轧制组织时,可能难以观测到局部焦耳热是否产生微小延展性差异。
600℃下沿X方向拉伸、Z方向压缩时,等效纯热场和脉冲电场的MD仿真结果如图8所示。仅凭此时的温度场已能给材料提供相当高的塑性。而当在X方向的真应变达到2,即工程应变达到6.39时,纯热场或脉冲电场辅助下变形仍然没有发生空位的聚集和断裂,这意味着此时局部焦耳热效应也难以对伸长率的提高起到额外作用。
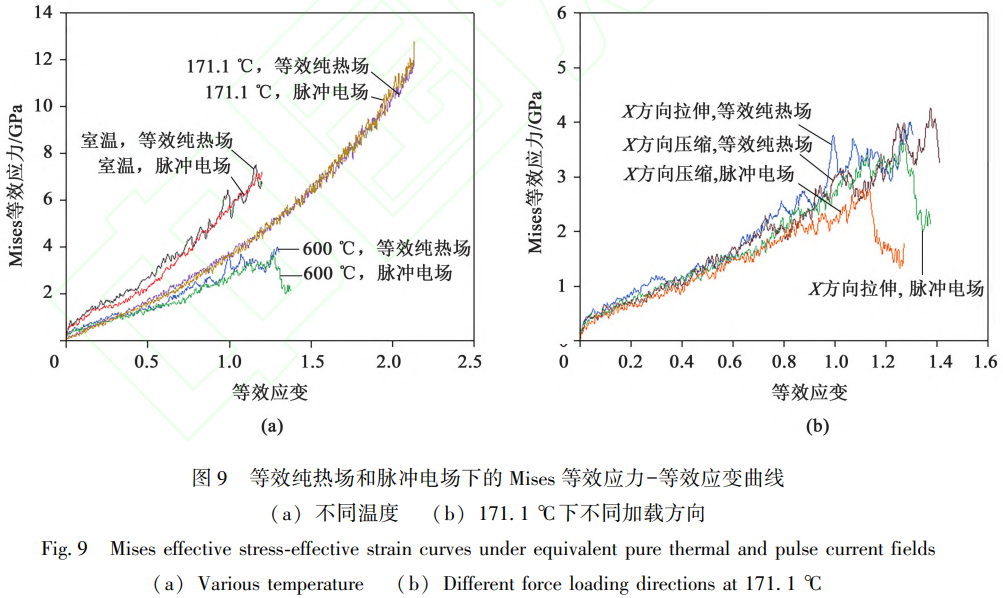
不同温度下沿X方向拉伸、Z方向压缩变形的Mises等效应力-等效应变曲线如图9a所示。在室温条件下,电场诱导的原子动能不均匀分布显著促进了流动应力的降低;随着温度升高至171.1℃,该效应仍然可见,但在600℃时差异基本消失。为量化局部焦耳热效应,定义“局部焦耳热比例系数”为同温度下考虑与未考虑该效应的应力比值,该系数在 20、 171.1和 600∘C下分别为 0.88、 0.91和0.97,表明局部焦耳热对流动应力的影响随温度升高而减弱。此外,在171.1℃下改变受力方向(改为沿X方向压缩、Z方向拉伸),比例系数变为0.85(图9b),说明该效应受晶向影响。然而,该效应对伸长率的提升不显著,在所有试验条件下均未观察到其对伸长率的改善,材料断后伸长率仍主要受整体的平均温度场影响。
2.2 FEM仿真结果
2.2.1基于单轴拉伸模型的 U形弯曲 FEM仿真
由于弯曲成形过程中模具左侧的圆角半径小于右侧,导致该侧板料会受到更大载荷,如图10所示。图11为室温、7.2A·mm²的有效电流密度加载下,Ti-6Al-4V钛合金板料U形弯曲在不考虑局部焦耳热效应时的等效塑性应变和Mises等效应力分布结果。考虑到所用板料的相对宽度(宽度/厚度)约为22.2,远大于宽板/窄板分界值3,因此,可认为所用的宽板在宽度方向上的变形受到约束,发生的变形很小,只需研究其正视图方向的截面即可。板料弯曲成形过程中,左侧的等效塑性应变和Mises等效应力明显更高,这是与其左侧变形更剧烈相对应。在成形结束时,等效塑性应变的最大值接近0.85,Mises等效应力的最高值则约900 MPa。
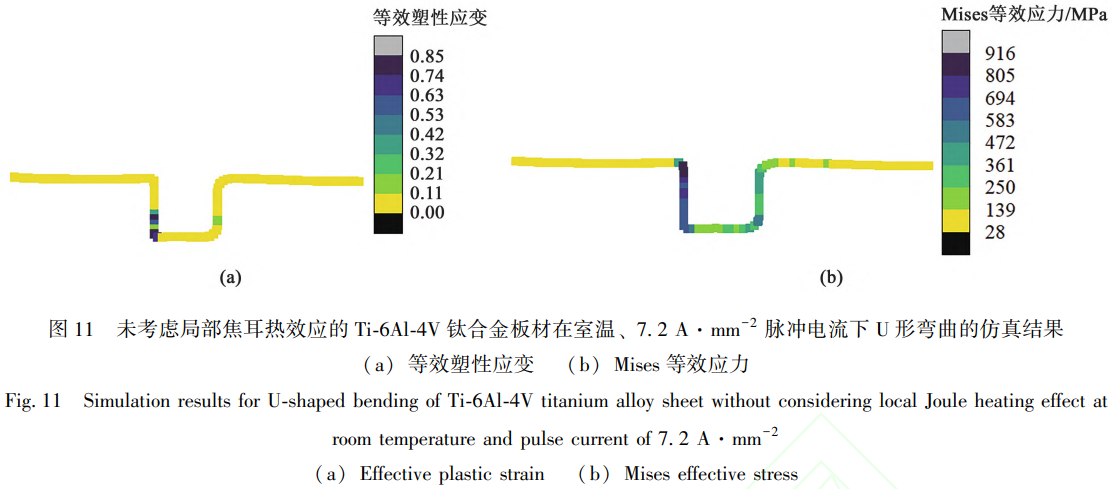
电流密度增长1.1A·mm−2使Mises等效应力降低约50MPa。Mises等效应力分布变化与等效应变的相似,变得相对地更为均匀。
同样在室温、有效电流密度为8.3A·mm−2下,Ti-6Al-4V钛合金板料U形弯曲的最大等效塑性应变降低至不超过0.70,对比图11a和图12a深色区域面积的对比,可直观地观察到,非热电致塑性效应带来的软化效果使得其整体变形更均匀。有效弯曲成形后移去模具,在隐式静力学下分析仿真回弹过程,得到两种有效电流密度下板料回弹后的形状及其相对位置关系如图10所示。较高的有效电流密度通过非热效应降低了流动应力,也同步地减少了回弹量。在弯曲件的两侧,两种板件的相对回弹量差值达到6.6mm。
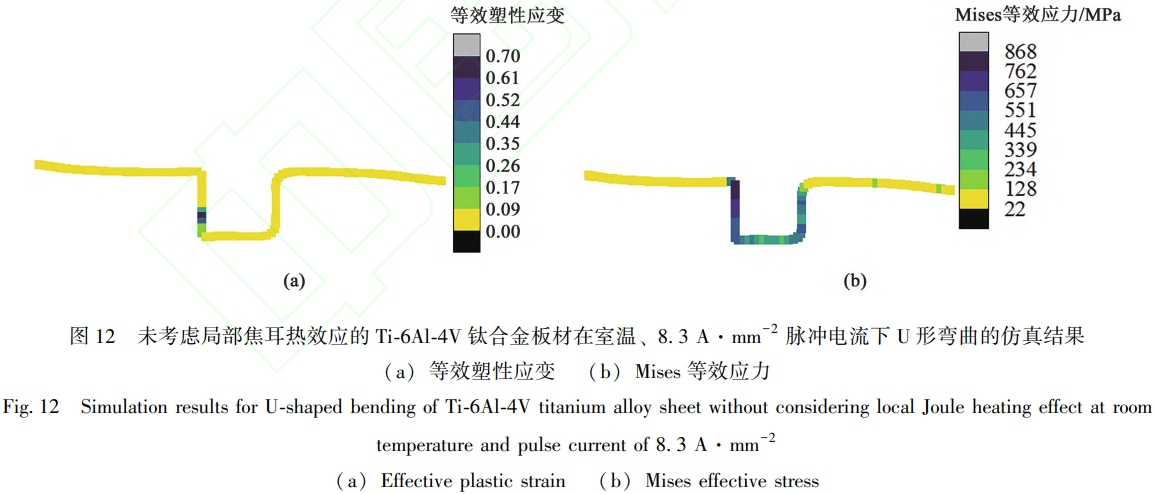
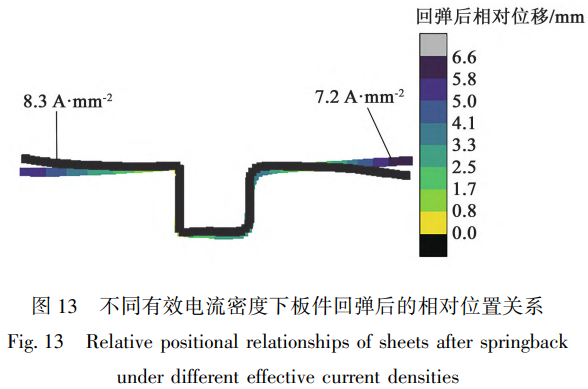
2.2.2经过MD仿真修正的电辅助U形弯曲FEM仿真
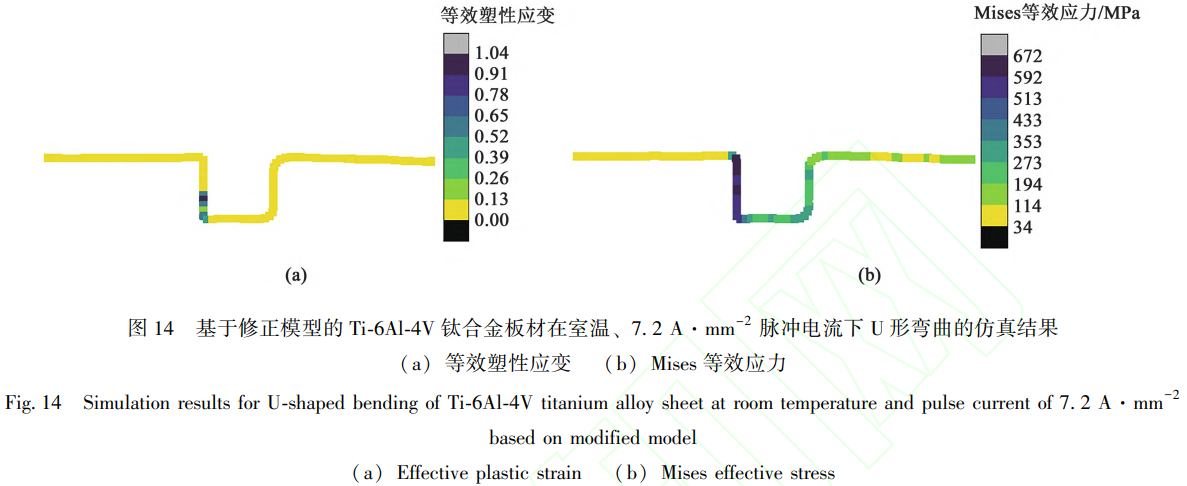
在实际的电辅助弯曲成形试验过程中,通过FLIR A655sc红外热像仪的测温,确认与模具接触位置的板料实际温度接近室温,因此假设是合理的。将Ti-6Al-4V钛合金室温单轴拉伸的曲线与室温的"局部焦耳热比例系数(0.88)”相乘,再去除式(2)和式(3)得到的应力降低值,即可利用MD方法得到电致原子动能不平衡的结果,以修正FEM仿真所用的本构关系。在此基础上,得到修正的室温、7.2A·mm²2下Ti-6Al-4V钛合金板料电辅助U形弯曲的等效塑性应变和Mises等效应力分布结果(图14)。等效塑性应变与修正前模型的分布情况相似,但应变值显著提高,最高等效塑性应变提高了约0.19,这意味着局部焦耳热效应促使发生更充分
的塑性变形,可获得更好的塑性。与图11b相比,Mises等效应力分布更为均匀,流动应力值也明显降低,修正的模型预测最大Mises等效应力降低了约244 MPa。应力分布更均匀和流动应力显著降低意味着修正模型预报的塑性更高,这归因于考虑了局部焦耳热效应。
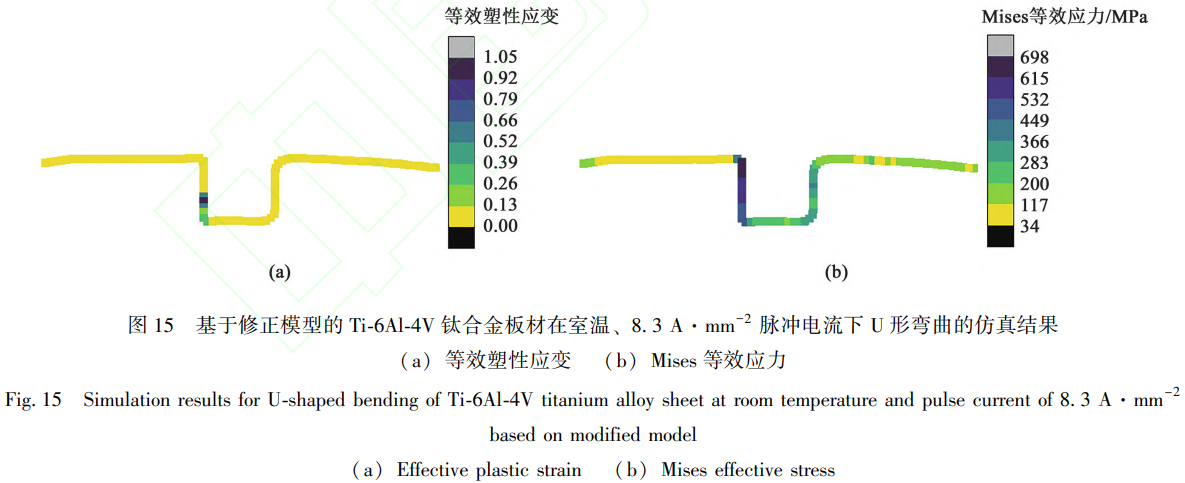
经过修正后,8.3A·mm²脉冲电流辅助成形仿真结果与脉冲电流为7.2A·mm²时相似,等效塑性应变分布结果非常接近(图15a)。Mises等效应力
也较为接近,相差不超过30 MPa(图15b)。但随着有效电流密度的提高,左侧板料边缘的Mises等效应力也有所提升,这意味着板料双侧变形更均匀。
基于修正模型,利用隐式静力学分析得到板料弯曲结束后的相对位移如图16所示。图16a中标明了U形自由端圆角1、2的位置。修正模型预测的回弹量明显增大,7.2A·mm²的有效电流密度下,最大相对位移达到14.0mm,而8.3A·mm−2的有效电流密度下,最大相对位移达到了30.6mm。值得一提的是,在8.3A·mm²的有效电流密度下,修正模型预测的U形回弹后形状有显著变化。
未考虑局部焦耳热效应模型和修正模型的弯曲
角及其相对实际试验结果的仿真误差如表1所示,括号内为回弹角度,正回弹角表示回弹后角度小于90°,负回弹角则表示回弹后角度大于90°。7.2A·mm²下未修正模型角1、角2的回弹预测误差分布为0.6%和15.7%;而修正模型角1、角2的回弹预测误差分别为0.3%和5.1%。8.3A·mm−2下,未修正模型预测误差更大,对于角2完全没有预测到回弹;而修正模型预测角度差值仅为1.78°,误差为22.7%。同时,未修正模型对角1的预测角度
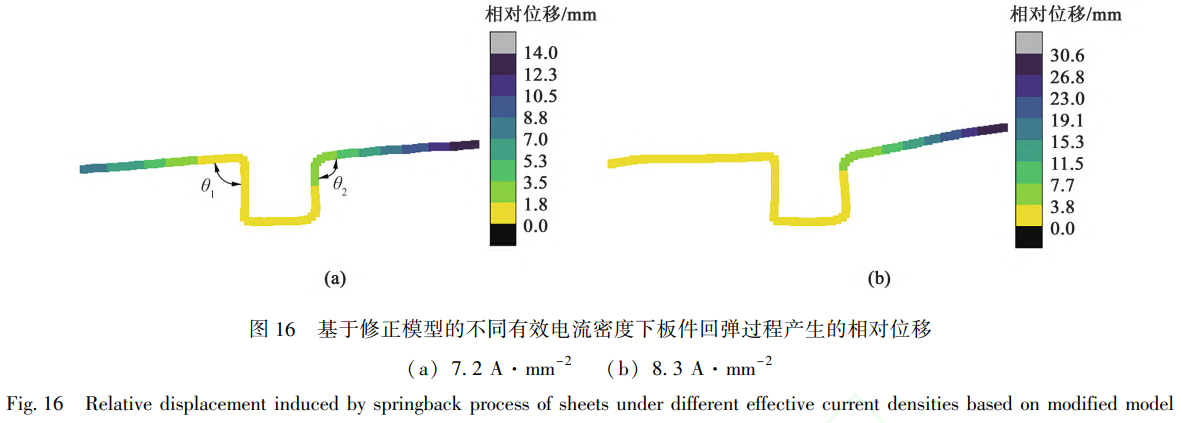
表1电辅助U形弯曲的角度
| 电流密度 | 测量角 | 原始模型预测/(°) | 修正模型预测/(°) | 试验数据/(°) | 原始模型预测误差/% | 修正模型预测误差/% |
| 7.2A·mm | 01 | 86.67(+3.33) | 86.64(+3.36) | 86.65(+3.35) | 0.6 | 0.3 |
| 7.2 A·mm | 02 | 101.13(-11.13) | 102.53(-12.53) | 103.20(-13.20) | 15.7 | 5.1 |
| 8.3A·mm | 01 | 88.28(+1.72) | 87.61(+2.39) | 87.05(+2.95) | 41.7 | 19.0 |
| 8.3 A·mm | 02 | 90.00(0) | 96.07(-6.07) | 97.85(-7.85) | 100.0 | 22.7 |
差值为1.23°,误差为41.7%;修正模型预测角度差值则降为0.56°,误差为19.0%,低于未修正时的一半。考虑了局部焦耳热效应的模型显著降低了预测误差,能够更准确地预测回弹值。
3、结论
(1)分子动力学仿真结果表明,由脉冲电场导致的原子动能不均匀分布(即局部焦耳热效应)能有效降低材料的流动应力。该效应在低温下尤为显著,其贡献可用“局部焦耳热比例系数”量化,其在室温、171.1和600℃下的平均值分别为0.88、0.91和0.97。
(2)局部焦耳热效应对于材料伸长率的提升作用有限,在某些加载路径下甚至可能不利于塑性。这表明,电致塑性的提升主要源于流动应力的降低,而非延展性的根本改善。
(3)借助分子动力学仿真获得了原子尺度局部焦耳热规律,并修正了宏观FEM仿真中的材料本构关系,从而构建了一个同时集成平均焦耳热、局部焦耳热及非热效应的力学模型。与未考虑局部焦耳热的模型相比,修正模型对弯曲角度的预测误差降低了至少一半。
参考文献
[1] Machlin E S. Applied voltage and the plastic properties of brittle rock salt[J]. Journal of Applied Physics, 1959, 30(7):1109-1110.
[2]翟奕涵,皇涛,邢兵辉,等.电辅助条件下钛-铝层状复合板力学性能与微观组织研究[J].精密成形工程,2025,17(8):1-11.
Zhai Y H, Huang T, Xing B H, et al. Mechanical properties and microstructure of titanium-aluminum laminated composite plates un-der electrically assisted conditions[J]. Journal of Netshape Form-ing Engineering,2025,17(8):1-11.
Ruszkiewicz B J, Grimm T, Ragai I, et al. A review of electrical-ly-assisted manufacturing with emphasis on modeling and under-standing of the electroplastic effect[J]. Journal of Manufacturing Science and Engineering,2017,139(11):110801.
[4]Okazaki K, Kagawa M, Conrad H. An evaluation of the contribu-tions of skin, pinch and heating effects to the electroplastic effect in tiatnium[J]. Materials Science and Engineering, 1980, 45(2):109-116.
Magargee J, Morestin F, Cao J. Characterization of flow stress for commercially pure titanium subjected to electrically assisted de-formation[J]. Journal of engineering materials and technology,2013,135(4):041003.
[6]Andre D, Burlet T, Korkemeyer F, et al. Investigation of the elec-[6] Andre D, Burlet T, Korkemeyer F, et al. Investigation of the elec-troplastic effect using nanoindentation[J]. Materials& Design,2019,183:108153.
[7]Sprecher A F, Mannan S L, Conrad H. Overview no. 49: On the mechanisms for the electroplastic effect in metals[J]. Acta Metal-lurgica,1986,34(7):1145-1162.
[8]Conrad H. Thermally activated plastic flow of metals and ceramics with an electric field or current[J]. Materials Science and Engi-neering: A,2002,322(1-2):100-107.
[9]Conrad H. Electroplasticity in metals and ceramics[J]. Materials Science and Engineering: A,2000,287(2):276-287.
[10]郑世龙,张宝,祖宇飞,等.工业纯钛TA1多物理场耦合拉伸变形行为研究[J].精密成形工程,2025,17(8):25-34.Zheng S L, Zhang B, Zu Y F, et al. Multi-physical coupled ten-sile deformation behavior of industrial pure titanium TA1[J].Journal of Netshape Forming Engineering, 2025, 17(8):25-34.
[11]张孟非.脉冲电流辅助钛合金塑性变形行为及电致塑性机理研究[D].太原:太原理工大学,2023.
Zhang M F. Pulsed Current-assisted Titanium Alloy Plastic De-formation Behavior and Electroplasticity Mechanism Study[D].Taiyuan: Taiyuan University of Technology,2023.
[12]杜引,赵亦希,于忠奇,等.2060-T8铝锂合金电致塑性本构方程[J].塑性工程学报,2017,24(1):133-139.
Du Y,Zhao Y X, Yu Z Q, et al. Constitutive equation of electro-plastic effect for 2060-T8 Al-Li alloy[J]. Journal of Plasticity Engineering,2017,24(1):133-139.
[13]翟瑞雪,吴庚洋,乔铮,等.TC4钛合金电致塑性本构方程建立[J].塑性工程学报,2024,31(3):91-99.
Zhai R X, Wu G Y, Qiao Z, et al. Establishment of constitutive e-quation of TC4 titanium alloy for electroplasticity[J]. Journal of Plasticity Engineering,2024,31(3):91-99.
[14] Hosoi A, Nagahama T, Ju Y. Fatigue crack healing by a controlled high density electric current field[J]. Materials Science and En-gineering: A,2012,533:38-42.
[15] Bhowmik A, Tan J L, Yang Y J, et al. Misorientation and disloca-Hosoi A, Nagahama T, Ju Y. Fatigue crack healing by a controlled
[J]. Journal of Materials Science& Technology, 2025, 209:292-299.
[16]Kim M J, Yoon S, Park S, et al. Elucidating the origin of electro-plasticity in metallic materials[J]. Applied Materials Today,2020,21:100874.
[17]王文波,张雪敏,王少阳,等.TC4钛合金方棒不同变形量对组织与性能的影响研究[J].锻造与冲压,2025(21):90-92.
Wang W B, Zhang X M, Wang S Y, et al. Studying of the effect of deformation amounts on the microstructure and properties of TC4 titanium alloy square bars[J]. Forging& Metalforming, 2025(21):90-92.
[18]Shim J, Ko W, Kim K, et al. Prediction of hydrogen permeability in V-Al and V-Ni alloys[J]. Journal of Membrane Science,2013,430:234-241.
[19]Fereidonnejad R, Moghaddam A O, Moaddeli M. Modified em-bedded-atom method interatomic potentials for Al-Ti, Al-Ta, Al-Zr, Al-Nb and Al-Hf binary intermetallic systems[J]. Computa-tional Materials Science,2022,213:111685.
[20]Wang J, Lee B J. Second-nearest-neighbor modified embedded-at-om method interatomic potential for VM(M=Cu, Mo, Ti) binary systems[J]. Computational Materials Science, 2021, 188:110177.
[21] Cao X D, An D Y, Liu Q, et al. Precipitation hardening charac-terization and stress prediction model in electrically-assisted Ti2AlNb uniaxial tension[J]. Intermetallics, 2024, 167:108214.
(注,原文标题:Ti-6Al-4V钛合金电致塑性变形的多尺度仿真研究)



yongyiti.com
永益钛手机网