引言
深海潜器作为深海科学探索与资源开发的核心装备,其结构安全性直接关系到潜器的服役性能以及人员的生命安全。然而,在极端高压环境下,深海潜器耐压结构有可能会因为几何缺陷、材料失效或是海底断崖等影响因素而导致灾难性的内爆,从而威胁到潜器的生命安全[1-3]。1963年,美国“长尾鲨”号核潜艇因海水管道损坏而诱发耐压结构内爆[4];2014年,美国“海神”号无人潜器因其携带的1472个陶瓷耐压结构发生连锁反应内爆,导致潜器在水下9900m处失事损毁[5];2023年,美国“泰坦”号观光潜艇在水下3800m处发生了内爆,艇上乘员无一生还[6]。因此,为避免因内爆事故而造成难以估量的损失,有必要针对深海高压环境下钛合金圆柱壳的内爆失效机制以及冲击特性开展相关研究。
脆性非金属材料耐压结构的水下内爆可以简化为同体积的气泡坍塌问题。Turner等[7]针对中空玻璃球开展了内爆试验,其通过水下压力传感器来监测内爆过程中的冲击波压力,并提出了一种考虑不同结构失效速率的内爆数值模拟方法。Diwan等[8]和Ling等[9]针对玻璃材质光电倍增管(photomultipliertube,PMT)的内爆特性开展了系统性的研究。Sun等[10-12]基于可压缩多相流理论并结合自适应网格技术,提出了一种基于有限元方法判断陶瓷耐压结构临界失效的内爆数值模型,并针对陶瓷耐压结构内爆、链式内爆和大规模殉爆问题进行了系统性的研究。Hu等[13]基于欧拉−拉格朗日耦合(coupledEulerian-Lagrangian,CEL)法建立了深海陶瓷耐压结构内爆的三相流固耦合数值模型,考虑了结构初始缺陷,并采用脆性陶瓷材料失效准则研究了不同触发方向下陶瓷耐压结构内爆的冲击波传播特性。
相对于脆性材料耐压结构,金属材料耐压结构的可靠性和安全性更高。Turner等[14]针对单一长径比的铝合金圆柱管开展了水下内爆试验和数值模拟研究,发现耐压结构内爆问题,特别是韧性材料耐压结构需要考虑流体与结构的相互作用。Farhat等[15]开展了不同长径比的铝合金圆管内爆试验,结果表明不同长径比金属圆管的坍塌模态不同,且压力脉冲持续时间和特征与金属管的坍塌模态有关。Muttaqie等[16]对铝合金圆柱壳和环肋圆柱壳等进行了一系列内爆试验,结果显示圆柱壳的极限强度与几何缺陷有关。Wu等[17-18]通过钛合金球形耐压壳的准静态压溃试验,发现钛合金球壳是先从应力集中区开始断裂失效,并分析了球形耐压壳水下内爆对临近结构的毁伤作用。Zheng等[19-20]开发了基于有限体积法和有限元法的流固耦合求解器,开展了潜器典型结构内爆问题数值模拟研究,并探究了钛合金球形耐压壳水下内爆对临近结构的冲击效应。在此基础上,Zheng等[21]又开展了钛合金球形耐压壳的水下内爆试验和数值模拟研究,发现了球形耐压壳内爆的垂向冲击效应。
尽管国内外学者针对深海非金属和金属材料耐压结构等的内爆问题开展了相关研究,但针对深海高压环境下钛合金圆柱壳内爆的研究相对较少,钛合金圆柱壳内爆过程中的流固耦合机制、冲击波演化规律、结构动态响应和能量平衡关系不清,内爆冲击特性及结构失效机制不明。因此,本文拟基于开源有限元求解器OpenRadioss,通过统一框架耦合自开发有限体积法可压缩多相流求解器和结构非线性有限元法求解器,并以深海钛合金圆柱壳为对象,开展多级静水压力作用下钛合金圆柱壳的内爆试验及数值模拟研究。首先,开展钛合金圆柱壳水下内爆试验,通过对比水下内爆试验结果验证数值方法的有效性;然后,分析钛合金圆柱壳内爆过程中的流场演化特性、结构非线性动态响应特征和能量平衡关系,探究多级静水压力对钛合金圆柱壳的结构失效机与内爆冲击特性的影响。
1、钛合金圆柱壳内爆试验
1.1试验试件及设备
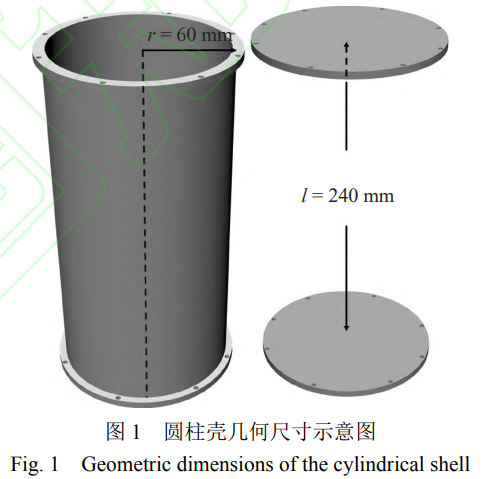
深海潜器需要在高静水压环境下长时间作业,极端恶劣的作业环境对耐压结构的材料和结构性能提出了极高的要求。钛合金TC4(Ti-6Al4V)作为一种α+β双相合金,兼具高强度、低密度、耐腐蚀等特点,被广泛应用于深海耐压结构制造[22]。因此,本文选用TC4作为圆柱壳材料来制备水下内爆试验试件,其几何尺寸如图1所示。钛合金圆柱壳的筒体外径r=60mm,筒体壁厚d=2.4mm,筒体长度l=240mm(长径比为2),由钛合金实心圆柱坯料经整体切削加工成形。筒体两端外置宽w=5mm、厚d1=5mm的连接法兰,并通过2个半径r1=65mm、厚d2=5mm的钛合金板式平焊法兰进行密封。
深海钛合金圆柱壳水下内爆试验采用上海交通大学的全海深深海环境模拟器,如图2所示。该装置包含电力驱动系统和试验系统2个部分,其中试验系统包括高压舱、密封盖和安全装置。

1.2钛合金圆柱壳水下内爆试验过程
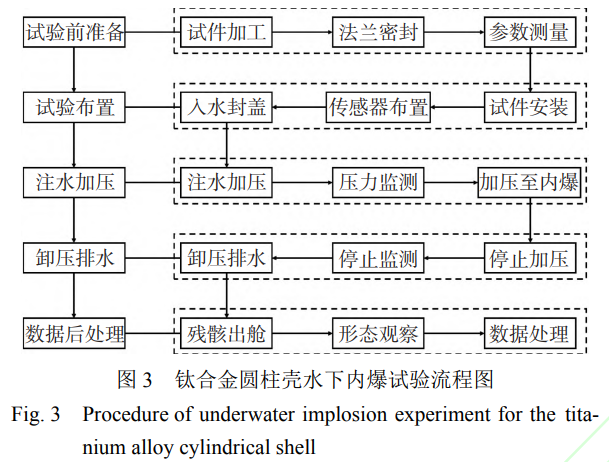
钛合金圆柱壳水下内爆试验流程如图3所示。在试验前,加工圆柱筒体、安装法兰密封并测量试件几何参数;随后,在水下内爆试验台架上安装试件及水下压力传感器,将试验台架通过起吊装置垂直静置于高压舱内,并采用密封盖和安装装置予以密封;接着,启动加卸载系统向高压舱内注水加压,同时开始监测舱内压力变化,待准静态加压至听到一声巨响后立即停止加压和对冲击波压力的采集;最后,卸压排水,打开密封盖取出试件残骸,然后观察试件残骸的形貌并对试验数据进行后处理。
在钛合金圆柱壳水下内爆试验过程中,圆柱壳通过钢丝固定在内爆台架中心,水下压力传感器则位于圆柱壳中心正上方距圆柱壳表面60mm处,如图4所示。

设试验加载速率为1MPa/min,当压力桶内的准静态静水压力达到钛合金圆柱壳的临界坍塌载荷时,圆柱壳内爆并释放高压高速冲击波。然后,通过水下压力传感器监测内爆过程中的冲击波动压(流体实际压力与静水压力之差),并采用高速动态数据分析仪进行内爆冲击波压力的采集。最终,钛合金圆柱壳在压力舱内压力达8.8MPa时发生内爆,试件残骸主要为3个大碎块,冲击波动压峰值为13.48MPa。
2、数值方法
2.1深海水下内爆可压缩多相流控制方程
深海钛合金耐压结构水下内爆问题涉及冲击波在水和空气中的传播,属于多介质非定常可压缩流体动力学问题,可以采用耗散界面多相流模型(diffuseinterfacemultiphaseflowmodel)[23-24]。该模型基于五方程模型,假设各相介质互不相容且在材料界面处无相对滑移,同时忽略流体流动过程中的黏性作用和表面张力效应。式(1)~式(5)为耗散界面多相流模型的数学形式,包括质量守恒方程、动量守恒方程、能量守恒方程和守恒形式的体积分数输运方程。
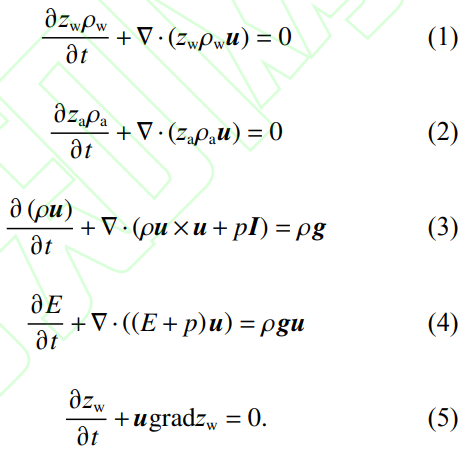
式中:∇为Nabla算子;t为时间;z为相体积分数;ρ为流体混合物密度;下标w,a分别代表水和空气这两相;ρw,ρa为相密度;u为流体混合物速度;g为重力加速度;p为流体混合物压力;I为单位矩阵。
为了避免守恒形式的体积分数输运方程在离散过程中引起非物理的数值振荡,需要采用非守恒形式的体积分数输运方程[25],如式(6)所示。
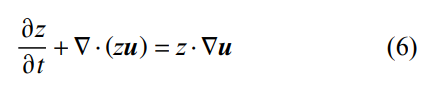
由于可压缩多相流控制方程为欠定方程组,故需建立物理闭合准则来实现模型的完备性。因此,采用理想气体和刚性气体状态方程分别对水和空气进行求解[26],如式(7)和式(8)所示。
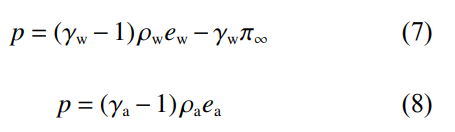
式中:γ为比热容比;e为单位质量的内能;π∞为压力常数。
2.2非线性动态响应方程与材料本构模型
钛合金圆柱壳在水下高压环境中发生内爆时,结构剧烈变形并高速坍塌,呈现出高度动态和强非线性特征。因此,采用显式非线性结构运动方程描述钛合金耐压结构的运动变形[21],其数学表达如式(9)所示。
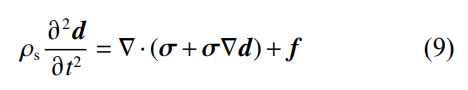
式中:等式左边表示由加速度产生的惯性力,其中ρs为结构密度,d为结构位移;等式右边第1项考虑了结构内部的力平衡,其中σ为结构应力,f为作用于结构上的外力。
在高静水压力作用下,钛合金耐压结构在内爆坍塌过程中存在弹性变形、塑性变形以及失效等多阶段动态响应行为,材料处于大变形、高应变率状态[27]。因此,使用Johnson-Cook本构模型和失效模型来描述深海钛合金耐压结构在水下内爆时的弹塑性变形和失效破坏。钛合金耐压结构材料的等效应力σeq如式(10)[28]所示。
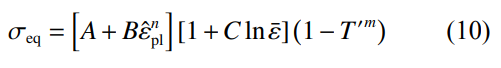
式中:A为屈服应力;B为硬化常数;为等效塑性应变;为等效塑性应变与参考应变的比值;n为硬化指数;C为应变率敏感系数;为无量纲温度;m为温度软化指数。
当结构所受应力达到其极限强度时,结构会发生断裂失效。因此,采用Johnson−Cook断裂准则来描述钛合金材料的失效和破坏。该准则使用与等效塑性应力相关的损伤变量D作为判断标准,初始值D0=0;当D=1时,结构失效断裂[29]。
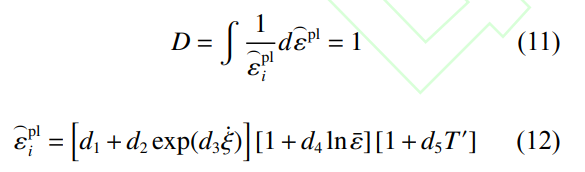
式中:
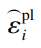 为失效时的等效塑性应变;,表示应力三轴度,其中为平均应力;d1~d5为失效模型参数。Johnson−Cook本构和失效模型参数的取值参考Lesuer[30]的试验结果,如表1所示。
为失效时的等效塑性应变;,表示应力三轴度,其中为平均应力;d1~d5为失效模型参数。Johnson−Cook本构和失效模型参数的取值参考Lesuer[30]的试验结果,如表1所示。
表 1 Johnson-Cook 本构和失效模型参数
| 参数 | 数值 | 参数 | 数值 |
| A/MPa | 862 | d₁ | -0.009 |
| B/MPa | 331 | d₂ | 0.25 |
| n | 0.34 | d₃ | -0.5 |
| C | 0.012 | d₄ | 0.014 |
| m | 0.8 | d₅ | 3.87 |
2.3水下内爆流固耦合
深海耐压结构内爆是涉及水、空气和结构三相耦合作用的复杂问题,内爆过程持续时间短,流体速度变化快,结构变形大,是一个瞬态、高雷诺数和强非线性的流固耦合问题。在数值模拟过程中采用任意拉格朗日欧拉方法(arbitraryLagrangian-Eulerian,ALE),通过统一框架耦合自开发有限体积法可压缩多相流求解器与结构非线性有限元法求解器,并采用罚函数方法处理界面穿透问题,从而实现对深海钛合金圆柱壳内爆流固耦合的数值模拟。
罚函数方法是通过拉格朗日乘子法在统一的虚功方程里添加罚函数项来实现,弱约束形式的虚功方程如式(13)所示[31]。
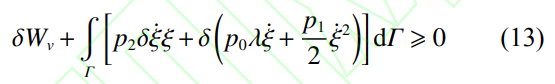
式中:Wv为功;δ为变分符号;λ为拉格朗日乘子;p0为拉格朗日乘子系数;p1为侵彻速率系数;p2为侵彻量系数;为流体与固体的耦合界面。当界面尚未发生侵彻(p2=0)时,接触力F的数学表达式为
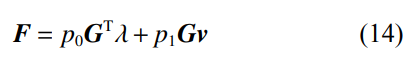
式中:G为约束矩阵;v为界面速度。当界面发生侵彻(p2≠0)时,接触力F的数学表达式为

式中:k为被穿透面刚度;dp为穿透深度。根据接触力F,即可求解每个显示时间积分步内流体和结构的运动方程。
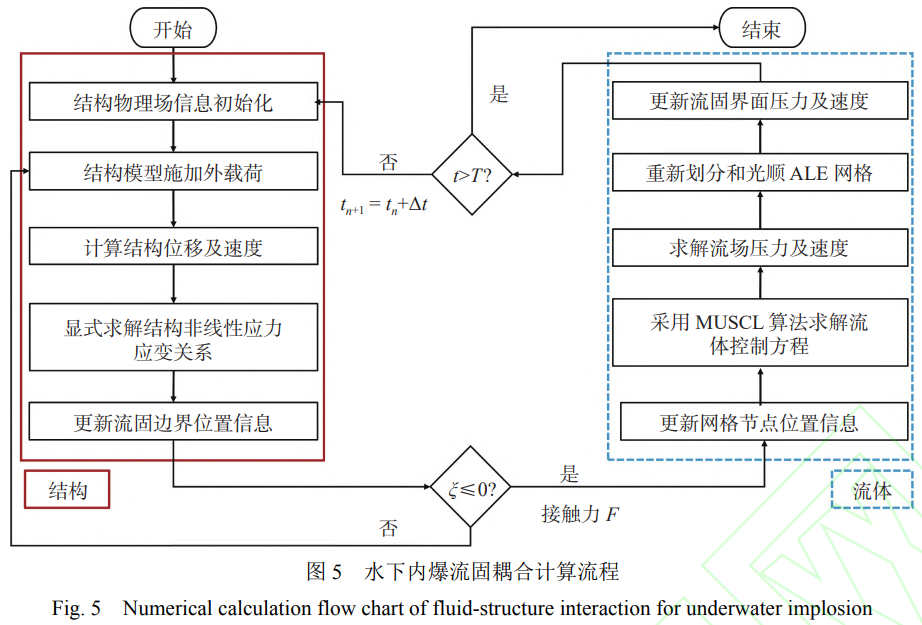
深海高压环境下钛合金圆柱壳的水下内爆流固耦合计算流程如图5所示。为了解决冲击波间断界面存在的非物理振荡现象,采用二阶迎风格式(monotonicupstream-centeredschemeforconservationlaws,MUSCL)对界面进行重构。在完成时间步tn的计算后,判断当前运行时间t是否小于预设总时间T,以决定是否进入下一时间步tn+1的计算,还是终止计算。
3、数值方法验证及算例设置
为了开展极端深海环境下钛合金圆柱壳的内爆失效机制以及冲击特性研究,首先需验证数值方法的准确性。通过对比深海钛合金圆柱壳的内爆试验结果,分别从耐压结构水下内爆结构坍塌形态和冲击波压力两方面对数值方法的准确性和可靠性进行验证。
3.1深海钛合金圆柱壳水下内爆数值模型
在进行深海钛合金圆柱壳内爆流固耦合的数值模拟时,采用半径为15r、长30r的圆柱形计算域;同时,为了避免内爆冲击波壁面反射的影响,设置了无反射边界条件[21],如图6所示。
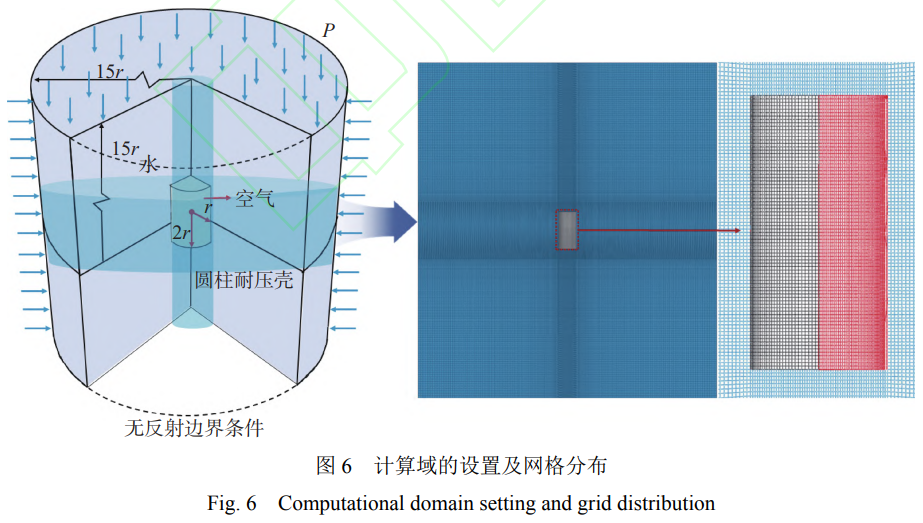
其中,圆柱壳位于计算域的中心位置,圆柱壳内、外分别为空气和水。空气域网格尺寸为1.5mm。为了减小计算量,降低网格数量,水域网格尺寸沿径向和轴向线性膨胀,膨胀比均为1.067,网格总量为982.1×104。将试验试件简化为两端端盖密封的圆柱壳,圆柱壳筒体几何尺寸与试验试件一致,端盖厚度与板式平焊法兰一致,均为5mm。圆柱壳网格尺寸为1.5mm,网格总量5.2×104。此外,依据《潜水系统与潜水器入级建造规范》,考虑了圆柱壳几何不圆度的影响[32],同时,还采用一阶屈曲模态位移结果的0.5%r作为圆柱壳的初始缺陷[18,21]。参考钛合金圆柱壳的内爆试验结果,数值模拟参数的设置如表2所示。
表 2 数值模拟参数
| 参数 | 数值 |
| 水密度 ρw/(kg・m⁻³) | 1000 |
| 水压力 Pw/MPa | 8.8 |
| 空气密度 ρa/(kg・m⁻³) | 1 |
| 空气压力 Pa/MPa | 1.013×10⁵ |
| TC4 弹性模量 E/GPa | 114 |
| TC4 密度 ρTC4/(kg・m⁻³) | 4430 |

3.2数值验证
钛合金圆柱壳内爆数值模拟与试验结果的结构变形特征如图7所示。尽管在数值模拟中结构碎片较多,但数值模拟的坍塌模式和变形形态与试验结果基本一致。导致两者差异的原因可能是在数值模拟中忽略了圆柱壳两端连接法兰对结构稳定性的强化作用,降低了结构强度。
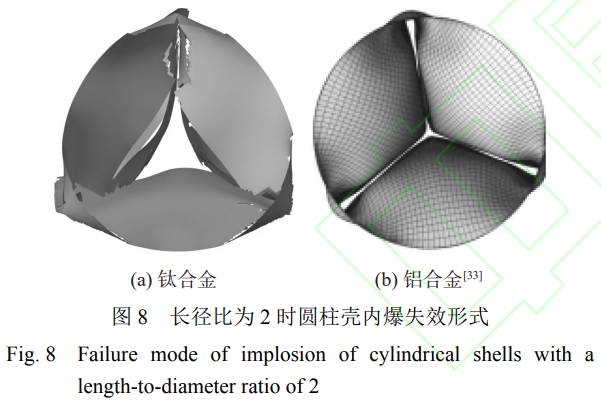
将钛合金圆柱壳内爆的数值模拟结果与Wang等[33]的研究结果进行对比。虽然长径比为2的钛合金圆柱壳在内爆时产生的小碎片较多,但钛合金圆柱壳以Mode3的形式内爆时与长径比为2的铝合金圆柱壳的内爆形式基本一致,如图8所示。
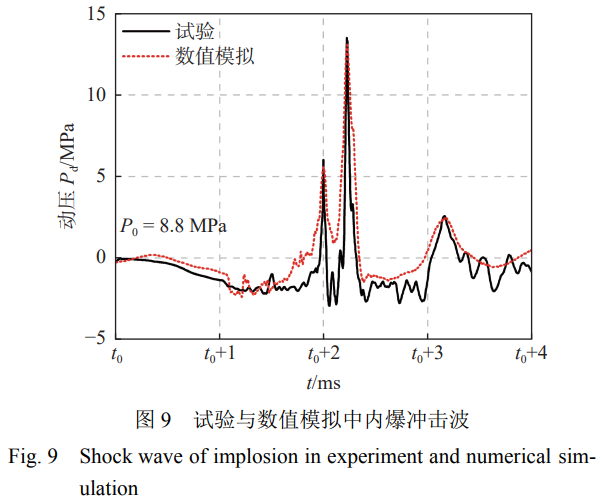
数值模拟与试验结果的流体动压力时程曲线如图9所示,其中t0为初始时刻。由图可见,二者的冲击波峰值分别为13.08MPa和13.48MPa,数值方法能够满足钛合金耐压结构水下内爆数值模拟的精度要求。
3.3网格收敛性分析及算例设置
为了保证数值模拟的精度,需要进行网格收敛性验证。定义收敛率Ri为[34]

式中,ε21=S2−S1,ε32=S3−S2,其中S1,S2,S3分别为粗、中、细3种网格尺寸下的数值模拟结果。
在进行钛合金圆柱壳内爆数值模拟网格收敛性验证时,压力监测点设置在+x方向上与圆柱表面相距r的位置上。结构内部空气域网格和外部水域的膨胀初始网格尺寸与结构网格尺寸的比例分别为,1和,膨胀比均为1.067,网格总数分别为756.4×104,982.1×104和1301.6×104。不同网格尺寸下的冲击波压力峰值和结构变形最大位移如表3所示,压力峰值的收敛率Rf=0.81,最大位移的收敛率Rs=0.25,均满足,满足收敛性要求。因此,本文采用1.5mm网格进行不同初始静水压力作用下钛合金圆柱壳的内爆数值模拟研究。
表 3 收敛性参数
| 网格比例 | 网格尺寸 /mm | 压力峰值 / MPa | 相对差值 ε | Rf | 最大位移 /mm | 相对差值 ε | Rs |
| √2 | 2.12 | 21.767 | - | - | 62.5 | - | - |
| 1 | 1.5 | 21.877 | 0.11 | - | 55.3 | -7.2 | - |
| √2/2 | 1.06 | 21.966 | 0.089 | 0.81 | 53.5 | -1.8 | 0.25 |
在进行深海钛合金耐压壳内爆试验时发现,相同尺寸的试件由于在加工工艺等方面存在差异,导致耐压壳的坍塌载荷存在差异[21]。因此,需研究多级静水压力下钛合金圆柱壳的水下内爆失效机制及冲击特性,算例设置如表4所示。表中,R,L分别为圆柱计算域的半径和长度。
表 4 水下内爆算例设置
| 算例编号 | 模拟水深 /m | 环境压力 / MPa | 结构尺寸 /mm | 计算域尺寸 |
| 1 | 880 | 8.8 | r=60.0;l=240.0;d=2.4;d₂=5.0 | R=15r;L=30r |
| 2 | 980 | 9.8 | r=60.0;l=240.0;d=2.4;d₂=5.0 | R=15r;L=30r |
| 3 | 1080 | 10.8 | r=60.0;l=240.0;d=2.4;d₂=5.0 | R=15r;L=30r |
| 4 | 1180 | 11.8 | r=60.0;l=240.0;d=2.4;d₂=5.0 | R=15r;L=30r |
4、结果与讨论
4.1水下内爆流固耦合流场演化特性
深海钛合金圆柱壳水下内爆流场演化过程如图10所示。为清晰展示水下内爆流场特性,取半径为6r的半球形流场进行分析。其中,为了分析流场随结构坍塌过程的演化规律,钛合金圆柱壳采用透明处理显示。
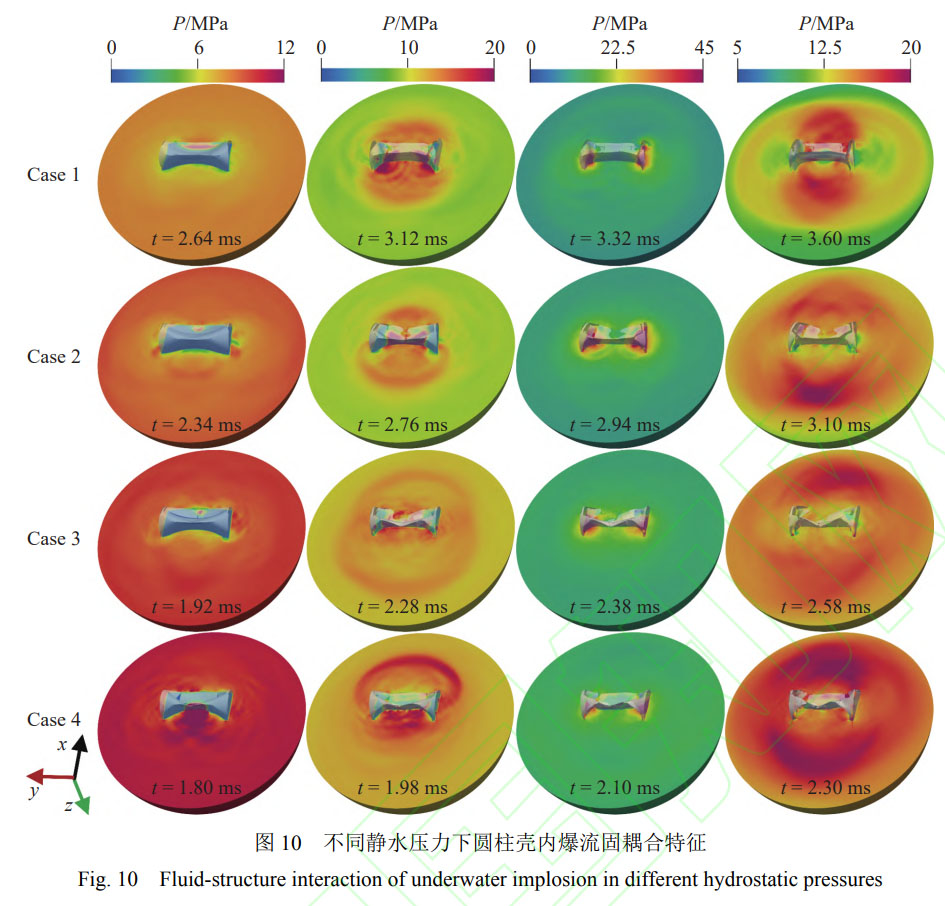
在静水压力作用下(Case1),圆柱壳向内变形,导致周围高压水向圆柱中心运动,圆柱附近流体的压力降低并产生稀疏波。结构在轴向上呈“三角”状坍塌,外部流体从裂缝流入圆柱壳内部,从而出现条带状的局部高压区(t=2.64ms)。不同方向的高速水流首先会在圆柱壳体中心碰撞,形成水锤效应,并首次产生内爆中心并向外释放冲击波(t=3.12ms)。此时,空气在圆柱两端形成低压区,诱使内爆中心由圆柱壳体中心向两端的低压区迁移。在高压水的作用下,圆柱两端继续坍塌,外部流体从圆柱中心及两端撕裂处流入,再次形成2个高压内爆中心(t=3.32ms)。同时,由于端盖阻碍了y轴方向的高压水运动,结构的非对称坍塌使内爆中心向−x方向偏移。最终,2个高压内爆中心会释放冲击波并向外传播,冲击波相互叠加并呈现出明显的方向性,致使圆柱壳周向(绕圆柱体轴线方向)上的冲击波压力较高(t=3.60ms)。
通过对比结构变形、流体运动及冲击波演化等流固耦合特征,发现不同静水压力下圆柱壳内爆的差异主要集中在两个方面:一是局部高压区和冲击波出现的时间提前,冲击波传播的非对称性更加显著,这是因为随着静水压力的增大,局部高压区的变化导致2次水锤效应的内爆中心位置发生迁移,在流体运动和结构变形的共同作用下,冲击波向外传播的非对称性显著;二是圆柱壳坍塌的模态相同但破碎形态不同,特别是圆柱壳−x方向上的大碎片逐渐从“弓”形转变成“M”形,这是因为静水压力的增大会导致圆柱向内坍塌的速度加快,结构破碎的程度增大,同时首次水锤效应的内爆中心由+x向−x方向迁移,导致内爆坍塌阶段结构在−x方向向内凹陷,因此随着静水压力的增大,结构破碎形态逐渐从“弓”形转变成“M”形。
4.2多相介质中非对称冲击波的传播与演化规律
在钛合金圆柱壳内爆过程中,2次水锤效应产生的内爆中心最大压力Pmax及最大无量纲压力P*max如图11所示,其中最大压力Pmax采用初始静水压力P0进行无量纲化,即P*=P/P0。
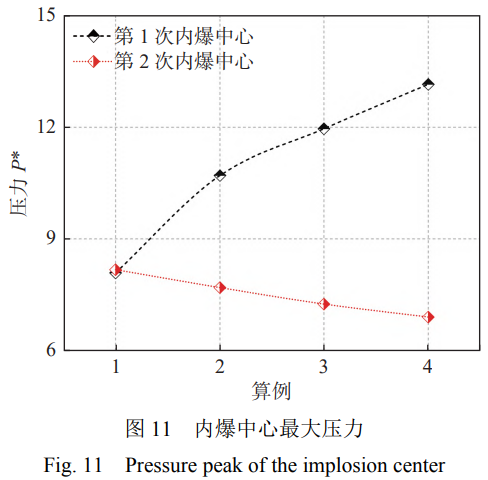
首次内爆中心的最大无量纲压力P*max1均随P0的增大而增大,最大增幅为62.6%。这是因为P0的增大使得圆柱壳坍塌的速度和高压水体向圆柱内部流动的速度增大,致使形成水锤效应时流体的碰撞更加激烈,导致P*max1均增大。然而,二次内爆中心的最大无量纲压力P*max2受P0变化的影响相对较小,其最大增幅为-15.5%。这是因为流体动能在首次内爆中心形成和传播的过程中,流体势能主要以冲击波的形式向外释放大量能量,导致后续的流体动能急剧减小。
为进一步探究多级静水压力作用下深海钛合金圆柱壳的内爆载荷特性,取距离圆柱径向和轴向距离为r的x+2r和y+3r的冲击波时程曲线进行分析,如图12所示。
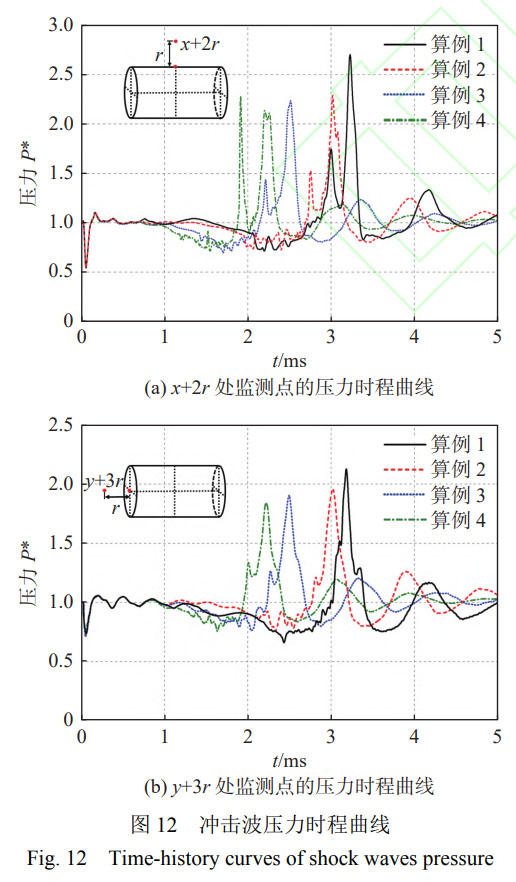
由图可见,在t=0.1ms时冲击波压力P*短暂降低,随后迅速恢复至初始静水压力。这是因为流体压力突然作用于结构,导致结构振动并产生了向外传播的稀疏波,从而使得流场压力降低。随后,P*迅速增大并达到第1个峰值P*1,此时高压水首先在圆柱壳中部相互碰撞并形成水锤效应,由此产生局部高压并释放向外传播的冲击波。接着,P*迅速降低随后急剧增大并达到第2个峰值P*2。这是因为圆柱壳被完全压溃时在圆柱两端二次内爆形成了水锤效应,导致在圆柱两端形成局部高压并向外释放冲击波。在y+3r处,未出现明显的峰值且冲击波峰值相对较小,这是因为内爆中心的迁移效应和端盖阻碍作用共同抑制了首次内爆冲击波在y方向的传播,同时也削弱了二次内爆冲击波的能量。
随着初始静水压力的增大,水下内爆流场低压持续的时间变短,冲击波峰值出现的时间相对提前,冲击波压力峰值逐渐降低。当静水压力为8.8~11.8MPa时,长径比为2的钛合金圆柱壳内爆在x+2r处的压力峰值P*随压力p的衰减可拟合为指数衰减函数P*max=5.414e(−p/7.318)+1,在y+3r处可拟合为指数函数P*max=2.609e(−p/10.222)+1。值得注意的是,在x+2r处11.8MPa下,P*1>P*2,这是因为随着初始静水压力的增大,内爆中心位置发生了变化,导致+x方向上的冲击波压力峰值相对较大。
4.3结构非线性动态响应及失效机制
为了探究多级静水压力下钛合金圆柱壳内爆过程中的结构失效机制,取不同时刻圆柱壳的变形云图进行了分析,如图13所示。
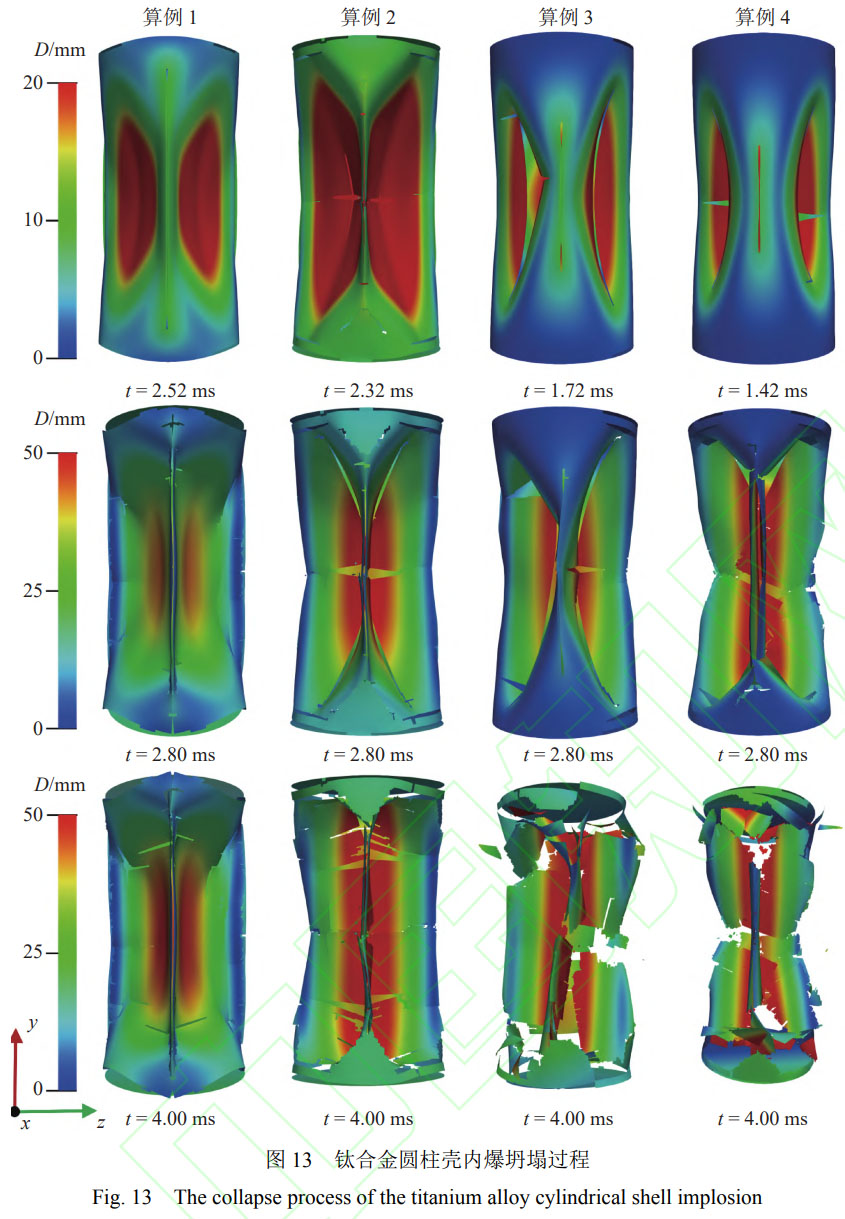
在外界静水压力作用下(Case1),结构在最大初始缺陷处首先出现局部应力集中而引发结构断裂,出现沿圆柱轴向延伸的裂缝(t=2.52ms),这种结构局部强度破坏导致的圆柱壳失稳坍塌是圆柱壳失效的主要机制。由于圆柱壳中部强度较低,其坍塌的速度明显快于圆柱壳两端,因此呈现出两端坍塌落后于中部的滞后现象。随后,在圆柱壳内、外高动水压差的持续作用下,端盖与筒体完全分离,圆柱壳呈一阶模态失稳并向内凹陷断裂成3个大碎块(t=2.80ms)。最后,3个大碎块相互碰撞形成大碎块和小碎片。其中,圆柱壳在−x方向上的大碎块相对完整;在+x方向上,2个大碎块碰撞会形成若干小碎片,并且存在明显的向内卷曲和局部撕裂现象(t=4.00ms)。
初始静水压力对结构动态响应的影响主要体现在3个方面:
1)静水压力影响圆柱壳的失效模式。静水压力增大到10.8MPa后,内、外压差的增大会引发圆柱壳的整体屈曲进而总体失稳,这是圆柱壳失效的另一机制。同时,局部应力集中位置发生变化、局部强度破坏和总体失稳的联合作用会导致圆柱壳失效模式从向内挤压变形变成向内卷曲变形。
2)静水压力会影响圆柱壳两端壳体坍塌的速度。这是因为随着静水压力的增大,圆柱壳失效机制由局部强度破坏主导逐渐变成总体失稳主导,导致壳体两端与中段的坍塌速度差相对减小,圆柱壳与端盖分离时的断裂现象更加显著。
3)静水压力影响碎块的数量和分布。随着圆柱壳内爆释放的冲击波能量增大,结构破碎的程度也随之增大,碎片分布更加集中。
4.4水下内爆能量平衡关系
图14所示为多级静水压力作用下流体动能(流体运动过程中的能量)和内能(流体所具有的势能)的演化曲线。
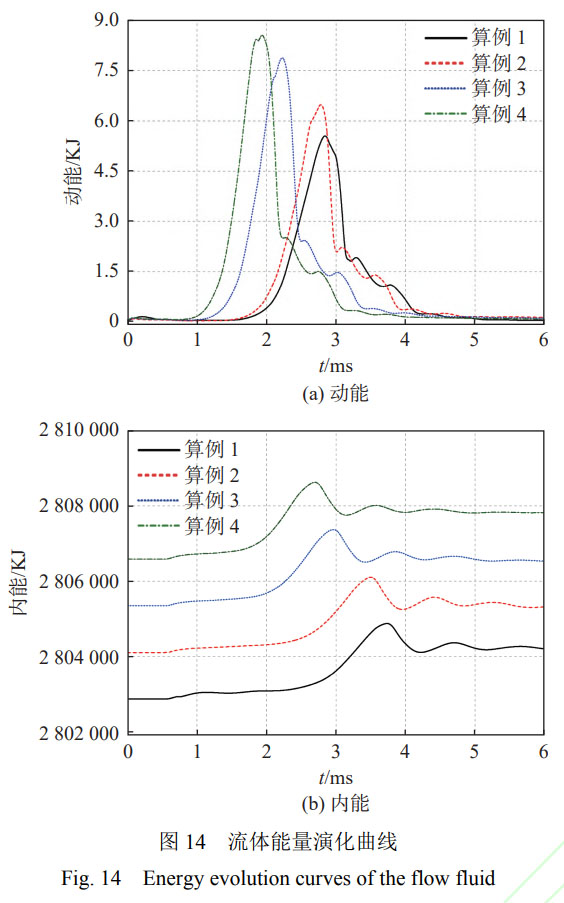
圆柱壳失效后,由于动压差的作用,外部高压水高速内涌,流体动能迅速增长,并在第2次内爆中心形成后达到峰值。随后,流体动能以冲击波的形式向外释放,因此,流体动能急剧衰减。内爆中心形成后,冲击波通过流体介质向外传播,因此,流体内能急剧增长并达到峰值。此后,由于气泡的脉动,流体内能呈现小幅波动现象。
随着静水压力的增大,内爆过程中的流体运动速度和动压差均增大,导致流体动能和内能增长量峰值均逐渐增大;此外,流体动能和内能峰值出现的时间均提前。
在水下内爆过程中,钛合金圆柱壳表现出显著的能量吸收特性,图15所示为多级静水压力作用下圆柱壳的动能(结构运动过程中的能量)和内能(变形过程中结构累积的能量)演化曲线。
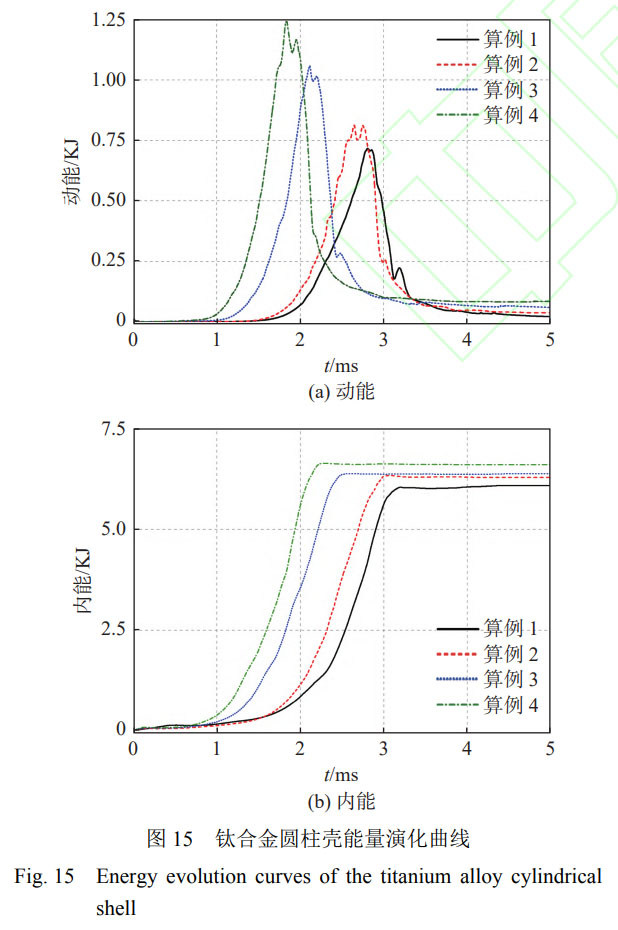
在钛合金圆柱壳水下内爆过程中,首先会发生弹性变形,此时结构运动速度极小,动能无明显变化。当壳体局部发生断裂时,高压水从裂缝处向圆柱壳内部高速内涌。随着圆柱壳坍塌速度的增大,结构动能急剧增长。首次内爆发生时,结构动能达到峰值并在极短的时间内保持高能量状态,随后急剧下降。这是因为首次内爆发生后,圆柱壳还未完全失效,流体会继续向内运动而引发二次内爆,在流体的冲击下结构继续运动,并在极短的时间内结构维持高动能状态。在外界高压静水作用下,圆柱壳先后经历弹性变形、塑性变形和断裂失效,其内能逐渐增大,在二次水锤效应后达到峰值并趋于平稳。
随着静水压力的增大,一方面结构动态响应速度增大,导致圆柱壳结构动能峰值出现的时间提前,结构内能更快地趋于平稳;另一方面,结构动能和内能的峰值均随静水压力的增大而增大。
5、结论
本文基于有限体积法求解了水下内爆可压缩多相流流场的高速运动,采用显式非线性有限元法求解了深海高压钛合金耐压结构坍塌失效的动态响应过程,系统性地分析了深海高压环境下钛合金圆柱壳的内爆冲击特性以及结构失效机制。同时,还开展了深海钛合金圆柱壳水下内爆试验,验证了采用自主开发的高分辨率任意拉格朗日−欧拉方法并结合罚函数方法求解水下内爆流固耦合的有效性。分析了钛合金圆柱壳在内爆过程中的流固耦合机制、多相介质中非对称冲击波的演化规律、结构非线性动态响应和能量平衡关系,探究了多级静水压力梯度下钛合金圆柱壳的内爆冲击特性及结构失效机制。主要结论如下:
1)钛合金圆柱壳先后两次形成内爆中心,首个内爆中心会随静水压力的增大发生显著的迁移效应。
2)随着静水压力的增大,钛合金圆柱壳的失效模式从向内挤压变成向内卷曲,破碎形态逐渐从“弓”形转变成“M”形。
3)长径比为2的钛合金圆柱壳的内爆展现出一阶模态失稳坍塌形式并形成了3个大碎块,且随着静水压力的增大,筒体端盖断裂现象更加显著。
参考文献:
[1]于爽, 胡勇, 王芳, 等. 全海深载人潜水器超高强度钢制 载人球壳的极限强度分析与模型试验 [J]. 船舶力学, 2019, 23(1): 51–57.
YU S, HU Y, WANG F, et al. Ultimate strength analysis and model tests for full-ocean-depth manned cabin[J]. Journal of Ship Mechanics, 2019, 23(1): 51–57 (in Chinese).
[2]王自力, 王仁华, 俞铭华, 等. 初始缺陷对不同深度载人 潜水器耐压球壳极限承载力的影响 [J]. 中国造船, 2007(2): 45–50.
WANG Z L, WANG R H, YU M H, et al. The Influence of the initial imperfections on the ultimate strength of manned deep-sea submersible pressure sphere hull[J]. Shipbuilding of China, 2007(2): 45–50 (in Chinese).
[3]郑建才, 贺宇培, 赵敏, 等. 深海钛合金耐压结构水下内 爆流固耦合动态响应机理研究 [J]. 海洋工程, 2025, 43(2): 54–67.
ZHENG J C, HE Y P, ZHAO M, et al. Study on the dynamic response mechanism of fluid-structure interaction in deep-sea titanium alloy pressure-resistant structures during underwater implosion[J]. The Ocean Engineering, 2025, 43(2): 54–67 (in Chinese).
[4]齐耀久. 美国海军"长尾鲨"级核潜艇 [J]. 现代舰船, 2004(10): 26−28.
QI Y J. “Thresher” class nuclear-powered submarine of the United States Navy[J]. Modern Ships, 2004(10): 26− 28 (in Chinese).
[5]CRESSEY D. Submersible loss hits research[J]. Nature, 2014, 509(7501): 408–409.
[6]PALMER C. Like the titanic, flawed engineering-and hubris-doomed the titan[J]. Engineering, 2024, 32: 1–3.
[7]TURNER S E. Underwater implosion of glass spheres [J]. The Journal of the Acoustical Society of America, 2007, 121(2): 844–852.
[8]DIWAN M, DOLPH J, LING J J, et al. Underwater implosions of large format photo-multiplier tubes[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2012, 670: 61–67.
[9]LING J J, BISHAI M, DIWAN M, et al. Implosion chain reaction mitigation in underwater assemblies of photomultiplier tubes[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2013, 729: 491–499.
[10]SUN S X, CHEN F H, ZHAO M. Numerical simulation and analysis of the underwater implosion of spherical hollow ceramic pressure hulls in 11000 m depth[J]. Journal of Ocean Engineering and Science, 2023, 8(2): 181–195.
[11]SUN S X, ZHAO M. Numerical simulation and analysis of the chain-reaction implosions of multi-spherical hollow ceramic pressure hulls in deep-sea environment [J]. Ocean Engineering, 2023, 277: 114247.
[12]SUN S X, ZHAO M, JIANG Y T. Numerical study of chain-reaction implosions in a spatial array of ceramic pressure hulls in the deep sea using a compressible multiphase flow model[J]. Physics of Fluids, 2024, 36(1): 016112.
[13]HU Y D, ZHAO Y F, ZHAO M, et al. Double ceramic sphere's sympathetic implosions triggered by local impacts [J]. Journal of Ocean Engineering and Science, 2023, 10(1): 59–69.
[14]TURNER S E, AMBRICO J M. Underwater implosion of cylindrical metal tubes[J]. Journal of Applied Mechanics, 2013, 80(1): 011013.
[15]FARHAT C, GERBEAU J F, RALLU A. FIVER: a finite volume method based on exact two-phase Riemann problems and sparse grids for multi-material flows with large density jumps[J]. Journal of Computational Physics, 2012, 231(19): 6360–6379.
[16]MUTTAQIE T, PARK S H, SOHN J M, et al. Implosion tests of aluminium-alloy ring-stiffened cylinders subjected to external hydrostatic pressure[J]. Marine Structures, 2021, 78: 102980.
[16]WU Y, DING J, WANG F, et al. Research on the quasistatic collapse and instantaneous implosion of the deepsea spherical pressure hull[J]. Marine Structures, 2022, 83: 103191.
[17]WU Y, LUO R L, WANG F, et al. Effect of the implosion of a deep-sea pressure hull on surrounding structures [J]. Applied Ocean Research, 2023, 132: 103477.
[18]WU Y, LUO R L, WANG F, et al. Effect of the implosion of a deep-sea pressure hull on surrounding structures [J]. Applied Ocean Research, 2023, 132: 103477.
[19]ZHENG J C, HE Y P, ZHAO M, et al. Dynamic response analysis of spherical pressure hull implosion inside adjacent underwater structure[J]. Ocean Engineering, 2023, 283: 115169.
[20ZHENG J C, LI M Y, HE T W, et al. The sympathetic implosion of multiple titanium alloy spheres under various inductive conditions[C]//Proceedings of the ASME 2024 43rd International Conference on Ocean, Offshore and Arctic Engineering. Singapore: American Society of Mechanical Engineers, 2024.
[21]ZHENG J C, ZHAO M. Fluid-structure interaction of spherical pressure hull implosion in deep-sea pressure: experimental and numerical investigation[J]. Ocean Engineering, 2024, 291: 116378.
[22]王硕, 梅志远, 付晓, 等. 无人潜器耐压壳体选型与承载 特征规律研究 [J]. 中国舰船研究, 2024, 19(4): 247– 253.
WANG S, MEI Z Y, FU X, et al. Pressure hull material selection and load law of unmanned underwater vehicle[J]. Chinese Journal of Ship Research, 2024, 19(4): 247–253 (in both Chinese and English).
[23]张阿漫, 明付仁, 刘云龙, 等. 水下爆炸载荷特性及其作 用下的舰船毁伤与防护研究综述 [J]. 中国舰船研究, 2023, 18(3): 139–154, 196.
ZHANG A M, MING F R, LIU Y L, et al. Review of research on underwater explosion related to load characteristics and ship damage and protection[J]. Chinese Journal of Ship Research, 2023, 18(3): 139–154, 196 (in Chinese).
[24]ALLAIRE G, CLERC S, KOKH S. A five-equation model for the simulation of interfaces between compressible fluids[J]. Journal of Computational Physics, 2002, 181(2): 577–616.
[25]JOHNSEN E, COLONIUS T. Implementation of WENO schemes in compressible multicomponent flow problems [J]. Journal of Computational Physics, 2006, 219(2): 715– 732.
[26]FLÅTTEN T, MORIN A, MUNKEJORD S T. On solutions to equilibrium problems for systems of stiffened gases [J]. SIAM Journal on Applied Mathematics, 2011, 71(1): 41–67.
[27]余 同 希 , 朱 凌 , 许 骏 . 结 构 冲 击 动 力 学 进 展 (2010- 2020)[J]. 爆炸与冲击, 2021, 41(12): 121401.
YU T X, ZHU L, XU J. Progress in structural impact dynamics during 2010-2020[J]. Explosion and Shock Waves, 2021, 41(12): 121401 (in Chinese).
[28]JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[J]. Engineering Fracture Mechanics, 1983: 541-547.
[29]JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures[J]. Engineering Fracture Mechanics, 1985, 21(1): 31–48.
[30]LESUER D R. Experimental investigations of material models for Ti-6Al-4V titanium and 2024-T3 aluminum [R]. Washington: Office of Aviation Research, 2000.
[31]BELYTSCHKO T, NEAL M O. Contact-impact by the pinball algorithm with penalty and Lagrangian methods [J]. International Journal for Numerical Methods in Engineering, 1991, 31(3): 547–572.
[32]中国船级社. 潜水系统和潜水器入级规范 [S]. 2018.
China Classification Society. Diving systems and submersibles classification and construction rules[S]. 2018 (in Chinese).
[33]WANG K G, LEA P, MAIN A, et al. Predictive simulation of underwater implosion: coupling multi-material compressible fluids with cracking structures[C]//Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering. San Francisco: ASME, 2014.
[34]CELIK I B, GHIA U, ROACHE P J, et al. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications[C]//Proceedings of the ASME 2007 Fluids Engineering Division Summer Meeting. San Diego: ASME, 2007.
(注,原文标题:深海高压环境下钛合金圆柱壳内爆失效机制及冲击特性研究)
无相关信息


yongyiti.com
永益钛手机网